skrypt093 (2)

180 Laboratorium Podstaw Elektrotechniki J

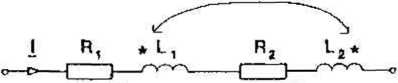
12.1.2.1. Połączenie szeregowe a)

M

Rj * L j

I ",    * L,

M

u,_    _Hi

^b)

Rys. 12.4. Szeregowe połączenie elementów magnetycznie sprzężonych: a) dodatnio (zgodnie), b) ujemnie (przeciwnie).

Dla wymuszenia sinusoidalnego w stanie ustalonym równania (12.3) i (12.4) można zapisać w postaci symbolicznej:

Ul = (Ri l-j o>L_t) I_L ±j-0)MI₂ = Zi-Il + Zm-12    O²’⁵)

L>2 = (R₂ + j f.) L₂) l2 ±j-w-M-I₁ =Z₂ l2 + Z.M ll    (12.6)

Zgodnie z prawami KirchhofTa dla sprzężenia zgodnego otrzymamy:

+U2 = [Rl +R₂+j-m-(Lł +L₂ + 2M)]I = Z_z1    (12.7)

natomiast dla sprzężenia przeciwnego:

li*=[R₁+R₂+j-«B-(Li+L2-2-M)].l-2p-I    (12.8)

Z zależności tych wynika, że wartość impedancji dla połączenia zgodnego (Z^) jest większa od wartości impedancji dla połączenia przeciwnego (Zp). Dla elementów indukcyjnych, których współczynnik sprzężenia nie ulega zmianie, można więc poprzez wyznaczenie impedancji dwóch połączeń określić zaciski jednoimienne,

Z równań (12.7) i (12.8) można wyznaczyć indukcyjność wzajemną M:

7—7    7 ^    7 ^

(12.9)

—7. -P    ~ ^AP

⁴-J-«    8-0J²-(Li + L₂)

12.1.2.2. Połączenie równoległe

Schemat połączenia równoległego dwóch cewek indukcyjnych sprzężonych magnetycznie przedstawia rys. 12.5.

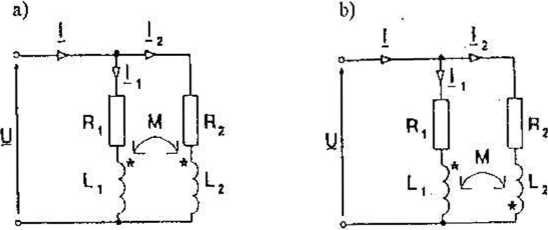
Rys. 12.5. Równolegle połączenie elementów magnetycznie sprzężonych: a) dodatnio (zgodnie), b) ujemnie (przeciwnie).

Zgodnie z prawami Kirchhoffa, uwzględniając zależności (12,5), (12.6) otrzymujemy wyrażenie:

(12.10)

u= ^ ^:^ZM² -1 = 2-1

—I^{+ 2}' 2m

przy czyni znak douczy sprzężenia zgodnego, natomiast znak "+" sprzężenia przeciwnego.

Z zależności (12.10) wynika, że impedancja zastępcza połączenia równoległego dwóch elementów indukcyjnych wynosi:

Z =

Z] + Z₂ + 2Z_m

(12.11)

a jej składowa czynna i bierna są zależne od pulsacji wymuszenia, co nic zachodzi przy połączeniu szeregowym.