skrypt159

164

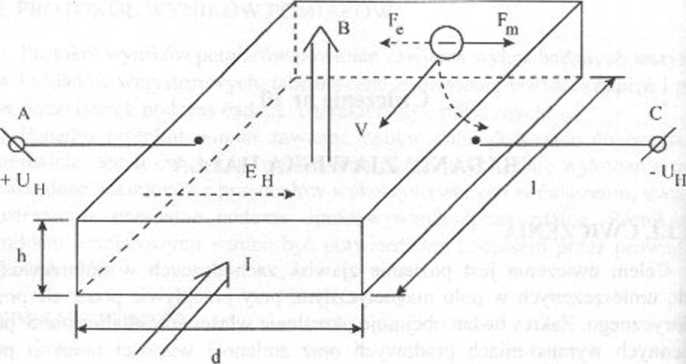
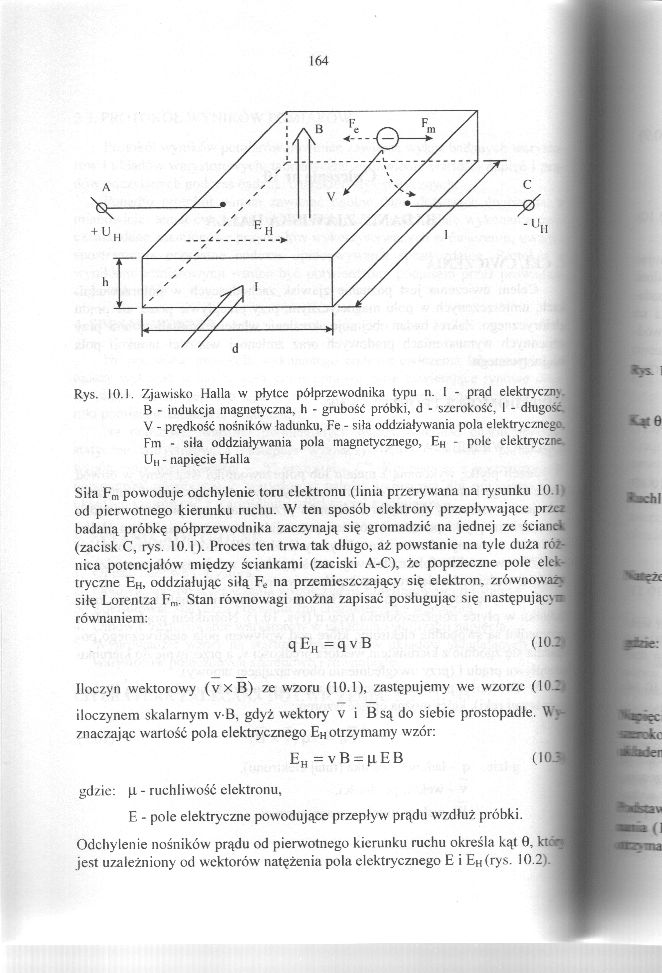
Rys. 10.1. Zjawisko Halla w płytce półprzewodnika typu n. I - prąd elektryce B - indukcja magnetyczna, h - grubość próbki, d - szerokość, I - długoś V - prędkość nośników ładunku, Fe - siła oddziaływania pola elektrycznej Fm - siła oddziaływania pola magnetycznego, F._H - pole elektryczne | Uh - napięcie Halla

Siła F_m powoduje odchylenie toru elektronu (linia przerywana na rysunku 10.1>J od pierwotnego kierunku ruchu. W ten sposób elektrony przepływające pr/c badaną próbkę półprzewodnika zaczynają się gromadzić na jednej ze śeii (zacisk C, rys. 10.1). Proces ten trwa tak długo, aź powstanie na tyle duża rc nica potencjałów między ściankami (zaciski A-C), żc poprzeczne pole el« tryczne E_H, oddziałując siłą F_ć na przemieszczający się elektron, /.równowa siłę Lorentza F_m. Stan równowagi można zapisać posługując się następując równaniem:

qE„=qvB

Iloczyn wektorowy (vxB) ze wzoru (10.1), zastępujemy we wzorze (1 OJ

iloczynem skalarnym v-B, gdyż wektory V i B są do siebie prostopadłe. W] znaczając wartość pola elektrycznego E_H otrzymamy wzór:

(10.

łi_H = v B = (i E B

gdzie: p - ruchliwość elektronu,

E - pole elektryczne powodujące przepływ prąciu wzdłuż próbki.

Odchylenie nośników prądu od pierwotnego kierunku ruchu określa kąt 0, jest uzależniony od wektorów natężenia pola elektrycznego E i E_H(rys. 10.2)

(1