skryptB

Rys 621

• Vf nnw* ru tha. i* ^DA^f^cyjNA srrnr rvvw

'kr	“T_L	}---«- n>.r i	1 (»-p?.r>'^ł
	Pot

RYS 6.19’ Sfkcj*łnk|«ll/uiv* nimj rtlynur>|n»-_B«.

Wówczas otrzymujemy poszukiwana zależność umożliwiającą adaptacyjne uaktualnianie parametrów filtru cstymacyjnego w postaci analng_IC7ne| .Jo (6 79,

YT

	_ .
^ror		_____

— • r

—— 'IV

RyS 6 20 Sclwm«lyr/nilrMli/«C|J «rkcii inicjalizuj,. f|

fił.r

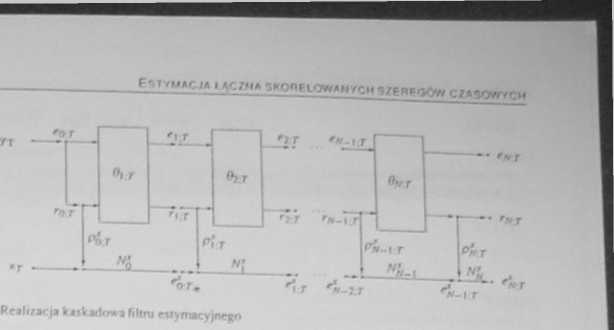
Realizacja kaskadowa filtru cstymacyjnego n(ilu M przyjmuje więc postać po kazana na rys 6.21 Podobnie jak przy implementacji algorytmu adaptacyjnej parametryzacji szeregów czasowych, nastawionej na realizację w czasie rzeczy wi.slyrn i przedyskutowanej w punkcie 6.3.2. celowe jest uzupełnienie przedsta wionego algorytmu filtracji rstymacyjnej o zależności umożliwiające adapta cyjnc uaktualnianie w czasie współczynników p’_r. określonych jak na razie - iloczynami skalarnymi (6 144) Postępując analogicznie, jak w cytowanym punkcie, wprowadźmy normalizację informacyjna rcsidualnych sygnałów pro pagowanyclt w dolnej gałęzi filtru z rys 0 21. to jest zdefiniujmy

P*.t Ph.t i!¹ -    r^|2! M • (^r«.r)^J)^ +«ń-i.z'».r    (6157)

a zależność (6 I48j przyjmuje ostateczna postać

^rn,T ~ (• ~ Irfj)⁷} ■ tl - (r.;z)²] -[ei-i.r-p;__rr,_;r]    (6.158)

analogicznie jak (6 80) Zależności (fi 157,-tfi. 158) stanowi, wiec- podstawę do realizacji adaptacyjnego filtru cstymacyjnego. nastawionej na działanie w czasie rzeczywistym i umożliwiającej dekompozycję równoległa i potok ou, algorytmu. Zauważmy, że realizacja taka wymaga trzech elementów pamięci na sekcję Inicjalrzacjc algorytmu wynikaj, z dyskusji działania filtru, analogicznej do przeprowadzonej w punkcie 6 3 3 Wynika z mej m in . że

•    eij._, = a-i =0

•    PZ.T ~ ⁰ dla n - T.....Mi T - 0.....M - I

I waga 1: W łagodnieniu filtracji odszumiającej sygnał {>-,) jest estymatorem szumu luh sygnałem odniesienia, o którym zakładamy, te jest obserwowany łącznic z pierwotnymi obserwacjami zawierającymi sygnał ( i,). który chcemy

estymować.

Uwaga 2: W zagadnieniu adaptacyjnego wygładzania (v,} jest sygnałem na w y/(ciii kanału. {t,} zai - pewnym znanym ciągiem uczącym

168

(((Kllll

Cyfrowa fiitracja adaptacyjna szEnEGów czasowyc i i

W podsumowaniu, algorytm filtru estyntacyjnego działa następująco Inicjallzacja dla T - 0:

Estymacja łączna skorelowanych szeregów czasowych

Algorytm:

•    I ■

•i

*

• yo =

• dane e, j. r„ r-i.p,+i r-i dian = 0,

M- I

dla n = -1_____

• algorytm:

.= a

* *« ' *

• *no = rn ' fn

•«*. 1.0“*"

■ I',

’ r.

- 0

o,

,M

-1=0, n - 0. ..M l Inicjallzacja dla T - 1,2,

• dane y_T. «_f

•ot = c)

’ Yt

a.

•r

••ot <ot Yl •<\t *F

Pn+i.T = Pu-it-i(I -e; _T |!( I - r; _r_,) • e, ^e»+t:ż = (I -Pe+ij) -U^-rA.r-i) ^[^r.r+(Vft.r^r«.r-tj ^rA+t.z = (l-p^i.p) ^(1-*;,r)'-[P"+i.reA.r+r.j--,j Pe T = P,*.ż-|[l - K-l:ż)^J]^|l ~(r..r)²}- +<-|_;zr«:T <J = (• - (f\'r>^?] *|l - (U:r)^J]-łK-_1:r - P^.r)

Vr = *r- ej.r

170