43972 statystyka skrypt30

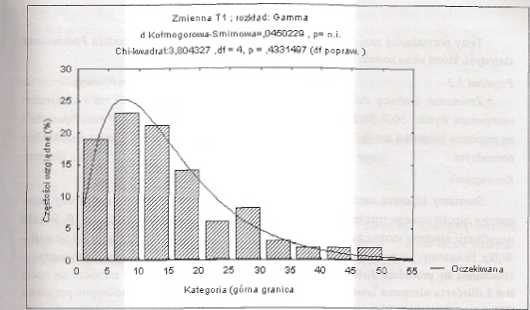
Rys. 3.3. Fuakcja gęstości rozkładu gamma z parametrami a ■ 2,0524697 i 0 =• 7,1431002 na tle histogramu częstości okresów trwilośd narzynek

Otrzymana wartość statystyki y² “ 3.804327 nie przekracza wartości krytycznej rozkładu x²- która dla 4 stopni swobody na poziomic istotności a * 0.05 wynosi x a. 4 = 9,488 (tablica BI), nie ma więc podstaw do odrzucenia hipotezy zerowej. Ten sam wniosek można wyciągnąć na podstawie obliczonej wartości poziomu istotności p = 0,4331497 dla uzyskanej wartości statystyki która to wartość p jest większa od przyjętego poziomu istotności a. a więc nie ma podstaw do odrzucenia hipotezy H»-

Podobnie, wartość statystyki testowej D_a = 0,0450229 testu Kołmogorowa jest mniejsza od wartości krytycznej testu Kołmogorowa, która dla próby o liczebności n = 100 wynosi D_0ln = 0,136 (tablica IV), a więc ten test też wskazuje, że nie ma podstaw do odrzucenia hipotezy zerowej. Prawdopodobieństwo p nie odrzucania hipotezy zerowej określone jest jako n.i., co oznacza nieistotny, a więc wartość statystyki D„ jest nieistotna. Wnioskiem końcowym może być stwierdzenie, że rozkład okresu trwałości narzynek może być opisany rozkładem gamma o wyżej obliczonych parametrach.

Należy tu podkreślić, że gdyby postawiono hipotezę zerową, że badana zmienna ma rozkład logarytmo-normalny lub dowolny inny z możliwych do wyboru, to końcowy wniosek równie dobrze mógłby być taki sam: nie odrzucać hipotezy zerowej. Wynika to z faktu, że test zgodności nie służy do rozróżniania dwóch lub więcej rozkładów lub pomocy w wyborze najlepszego rozkładu spośród zaproponowanych. Celem tego testu jest tylko odpowiedź na pytanie: Czy mogę przyjąć rozkład, który skłonny jestem uznać za właściwy lub czy dane są na tyle niezgodne z proponowanym rozkładem, że muszę go odrzucić?

39