SNC00705

i a) przy jednokrotnym rzucie symetryczna monetą:

³ wpadł    .<»,«! («**■', lub w skrócie ru, = 0, w,= Si

U~ (lwpadł    j, (wypadła <%ot\A*    )> lub w skrócie 12 - {O . ^ j

bł przy dwukrotnym rzucie monetą (lub dwiema monetami, które rozróżniamy):

Iwymk pierwszego rzutu ©•erwsza monetat	Wynik drugiego rzutu (druga moneta) orzeł (0) reszka (R)
orzeł (0) reszka w	{0.0) i V'\

a^io.cMo^Ko),^    }

2.Z pudelka (umył, w której znajduje się po kilka takich samych kul białych I czarnych, łosulemy dwukrotnie (koleino) pó jednej kuli. Przebieg I wynik tego doświadczenia losowego możemy przedstawić graficznie (drzewkiem).

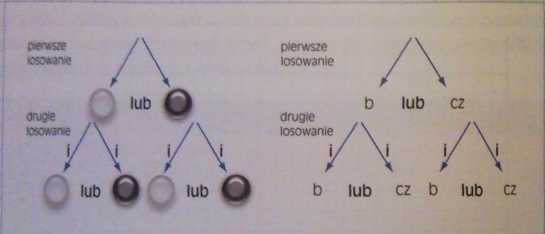
Oczytaj i wypisz zbiór zdarzeń elementarnych tego doświadczenia.

rzyktad. (za pierwszym razem wylosowano kulę białą, za drugim razem wylosowano białą)

owa rożne swetry i trzy pary różnych spodni? rżeń elementarnych.

Para spodni	Sweter S, Si	A
P,		s, lub s,
Pi		/
Pj		Pi
{{PrSy}.

Uzupełnił graf l tabele. Wypisz zbiór zda-

4. Ile można utworzyć liczb dwucyfrowych z cyfr 1,2,3: a) gdy cyfry w liczbie mogą sle powtarzać?

Uzupełnił graf (drzewko) I podą) zbiór zdarzeń elementarnych,

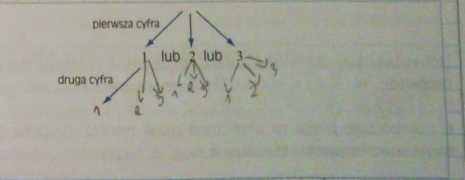
n={

Wypisz te liczby:

b) gdy cyfry w liczbie nie mogą się powtarzać?

Uzupełnij graf (drzewko) i wypisz te liczby (zbiór zdarzeń elementarnych),

pierwsza cyfra

druga cyfra

t'

i lub

I

2

i

lub 3

ll

Mczbe