str068 (2)

uui piiry woan«i|, po poilnlnwlBiiIu (f»liii) ilu (fi mu

A

'r

10 "    12.00/' l I /IN KI ,

_r \ ■//

5 sin VE‘ -1-2.25

(5.70)

I )ln obliczenia obu opóźnień wystarczającym jest pomiar: temperatury (T), ciśnienia (P) oraz ciśnienia pary wodnej e_p .

5.3.4. Model Saastamoinen

W przeciwieństwie do modelu empirycznego Hopfield’a, algorytm ten oparty jest na rela-cjnch wynikających z analiz fizycznych praw gazowych. W rozważanym podejściu opóźnienie Iroposferyczne, wyrażone w metrach, opisane jest zależnością

A r -

0.002277

cos

(z)

f 1255 ^P+{—

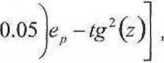
(5.71)

gdzie:

/» - ciśnienie [mbar],

/ temperatura [K],

• odległość zenitalna satelity, i), - ciśnienie pary wodnej [mbar].

Model ton został poprawiony przez Bauersima przedstawiając poprawkę jako

A, =

0.002277

cos

(^z) _

p⁺

(1255 T

+ 0.05

;

e -B lg²(z) fV(ę,h)+8R

(5.72)

gd/la:

II - wartości empiryczne (B jest funkcją wysokości miejsca obserwacji),

iiH - funkcja wysokości oraz odległości zenitalnej satelity,

lł’(<p,/i) poprawka grawitacyjna zależna od szerokości geograficznej i wysokości.

Wartości współczynników: B, 8/? zaprezentowano w poniższych tabelach.

lub 5.2. Wartość współczynnika B w funkcji wysokości dla modelu Saastamoinen

h - wysokość [km]	B [mb]
0.0	1.156
0.5	1.079
1.0	1.006
1.5	0.938
2.0	0.874
2.5	0.813
3.0	0.757
4.0	0.654
5.0	0.563

MU

luli 5,3 Wartość wipólc/ynnlkn 6W w funkcji wywolM»»»•:! dln tru idolu tłaiuitnmolnon

Wysokość powyłnj pn/loimi morJin |km)

Z	0,0	0 5	1.0	1.6	2 0	3.0	4.0	5.0
60“00'	0.003	0.003	0.002	0.002	0.002	0.002	0.001	0 001
66“00'	0.006	0.006	0.005	0.005	0.004	0.003	0.003	0.002
70°00'	0.012	0.011	0.010	0.009	0.008	0.006	0.005	0.004
73°00'	0.020	0.018	0.017	0.015	0.013	0.011	0.009	0.007
75“00'	0.031	0.028	0.025	0.023	0.021	0.017	0.014	0,011
76°00'	0.039	0.035	0.032	0.029	0.026	0.021	0.017	0,014
77"00' .	0.050	0.045	0.041	0.037	0.033	0.027	0.022	0.010
78°00'	0.065	0.059	0.054	0.049	0.044	0.036	0.030	0.024
78°30'	0.075	0.068	0.062	0.056	0.051	0.042	0.034	0,028
79°00'	0.087	0.079	0.072	0.065	0.059	0.049	0.040	0.o:i:i
79°30'	0.102	0.093	0.085	0.077	0.070	0.058	0.047	0.030
79°45'	0.111	0.101	0.092	0.083	0.076	0.063	0.052	0 043
80°00'	0.121	0.110	0.100	0.091	0.083	0.068	0.056	0 04 /

Przedstawione tu dwa z wielu istniejących modeli troposfery oczywiście nie wyc/iiipiiju / gadnienia. Istnieje wiele modeli (Chao - 1972, Marini i Murray - 1973, Goud I i iooilmnn 1974, Black - 1978, Lanyi - 1984, Davis - 1985, Robinson - 1986, Rahnomoon I*u Spilker- 1996), które z różnym powodzeniem stosowane są w pomiarach GPS,

Odmiennym podejściem dla oszacowania opóźnienia troposferycznego Jest primlei /.iw, tości pary wodnej wzdłuż trasy propagacji fali radiowej transmitowanej prze/ sfilolllę. < ieln temu służy radiometr pary wodnej. To niezmiernie kosztowne urządzenie umożliwia pomlui wysokości ok. 12 km. Zastosowanie tego przyrządu umożliwia zmniejszenie błędu lropm.li do wartości ok. 1-2 cm. Dla porównania zastosowanie modelu niweluje błędy do po/loi 2-5 cm.

5.4. Wielodrogowość (wielodrożność) sygnałów GPS

W radiokomunikacji ruchomej, której najlepszym reprezentantem wśród systemów nm gacyjnych jest GPS, lokalne warunki odbioru sygnałów niejednokrotnie decydują o jako połączenia radiowego, co w radionawigacji przejawia się poprzez jakość rozwiązaniu po/yc nego. Uwarunkowania lokalne, szczególnie w nawigacji lądowej, mogą wpływać wręcz decyi jąco na dokładność wyznaczenia współrzędnych. Głównym czynnikiem decydującym o dok dności wyznaczeń pozycji w mieście, rzutując w wyraźny sposób na rozwiązania technlo/i jest tzw. efekt wielodrogowości lub wielodrożości sygnałów GPS (ang.: multipath). Wskul tego zjawiska sygnały satelitów na drodze do anteny odbiornika mogą zostać odbite od pi. szkód terenowych, budynków lub powierzchni znajdujących się w jej pobliżu (rys. 5.3).

Dla pomiarów kodowych - stanowiących podstawową metodę pomiarów nawigacyjny, w wyniku wielodrogowości sygnałów można spodziewać się nawet błędów 20-30 m dla pti dynczych pseudoodległości. Jednakże w wyjątkowo niekorzystnych warunkach określany terminem: urbanistyczny kanion - sięgać mogą one nawet do 100 m. Przy tym rzędzie błęd relatywnie łatwo pomylić sąsiadujące ze sobą ulice - co dla systemów lądowych skutk koniecznością stosowania dodatkowych sensorów prędkości oraz kierunku wspomagany bieżącym zliczeniem drogi w oparciu o mapę wektorową. Dia nawigacji morskiej i lotnie wielodrogowość sygnałów może być łatwo usunięta poprzez właściwą instalację antę