ullman131 (2)

wanic poszczególnych krotek. Jeśli natomiast traktujemy relację jako zbiór, to musimy zawsze porównywać wynik rzutowania składowych poszczególnych krotek z dotychczasowym wynikiem rzutowania, po to by upewnić się, źc nowa krotka jeszcze nie jest dołączona do wyniku. Jeśli jednak dopuszcza się wielozbiór jako postać wyniku, to po prostu wykonuje się rzutowanie i powstałą krotkę dołącza do wyniku, nic potrzeba już porównywać nowej krotki z dotychczas uzyskanymi.

PRZYKŁAD 4.48

Jeśli założymy, żc wynikiem rzutowania może być wielozbiór. to można traktować wielozbiór przedstawiony na rys. 4.28 jako wynik rzutowania relacji pokazanej na rys. 4.29 na atrybuty // i B. Jeśli natomiast potraktujemy operator rzutowania tak jak w algebrze relacji i w związku z tym wyeliminujemy powtarzające się krotki, to uzyskamy następujący wynik:

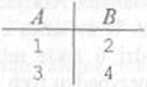
Zauważmy, iż mimo tego, że wielozbiór zawiera więcej elementów, wynik można uzyskać szybciej, ponieważ nic trzeba każdej z krotek (1, 2) i (3, 4) porównywać ze wszystkimi, które zostały dotychczas wygenerowane.

A	B	c
1	2	5
3	4	6
1	2	7
1	2	8

RYSUNEK 4.29 Wielozbiór z przykładu 4.48

Ponadto, jeśli celem rzutowania jest uzyskanie pewnej zbiorczej wartości (będzie o tym mowa w podrozdziale 5.5), na przykład zadanie polega na: ..znaleźć wartość średnią składowych A relacji przedstawionej na rys. 4.29", to nie możemy traktować rzutowanej relacji w terminach zbioru. Jeśli bowiem będziemy stosować tu model zbioru, to wartością średnią A będzie liczba 2, ponieważ na rys. 4.29 występują tylko dwie różne wartości tego atrybutu. I oraz 3, co daje średnią 2. Jeśli jednak potraktujemy kolumnę A i ry s. 4.29 jako wielozbiór {1,3, 1. I}, to otrzymamy poprawną wartość średniej 1,5.

□

Drugi przypadek, kiedy dopuszczenie wiclozbioru w postaci wyniku umożliwia zaoszczędzenie czasu przetwarzania, zachodzi, gdy oblicza się sumę dwóch relacji. Jeśli upieramy się prz> traktowaniu relacji R u ó’jako zbioru, to

każdą krotkę t S musimy sprawdzać, czy nic należy ona jednocześnie dc Jeśli tak się zdarzy i okaże się. że pewna krotka r S należy również do relacj lo ta krotka nie zostanie dołączona do sumy, w przeciwnym razie zostanie d czona do sumy. Jeśli natomiast pozwolimy, aby w wyniku sumowania pow wielozbiór, to po prostu skopiujemy wszystkie krotki z relacji R i wszy* krotki z relacji S do wyniku, bez względu na to, czy' są takie same, czy’ nic.

4.6.2. Suma, przecięcie i różnica wiclozbiorów

Przy obliczaniu sumy dwóch wiclozbiorów dołącza się wszystkie wy pienia krotki z poszczególnych składników sumy. Oznacza to, że jeśli w r cji R krotka t powtarza się n razy, a w relacji S m razy, to w sumie relacji _t S krotka t występuje n + m razy. Oczywiście zarówno n. jak m_t a także ( zmienne jednocześnie mogą mieć wartość 0.

Przy przecięciu wielozbiorów. w których krotka t występuje odpow nio n i m razy' w wielozbiorach R i S, to w ich przecięciu R r\ S krotka / stępuje min(n, m) razy. Z kolei, jeśli obliczamy różnicę R S, to tam krot występuje max(0, n m) razy. Oznacza to, żc jeśli w relacji R jest więcej stąpień krotki t niż w relacji S, to w różnicy R S liczba wystąpień kroi jest równa różnicy jej wystąpień w R i S. Jednakże jeśli w relacji S krot występuje tyle samo razy co w krotce R, to w różnicy R S krotka / wcale wystąpi. Mówiąc obrazowo: każde wystąpienie krotki / w wielozbiór* kasuje jedno jej wystąpienie w zbiorze R.

1'RZYKLAD 4 49

Załóżmy, żc relacja R jest taka. jak na rys. 4.28, tzn. składa się ona / tr, wystąpień krotki (1.2) oraz jednego wystąpienia krotki (3. 4). Z kolei ó wicra następujące dane:

n

2

4

4

6

A_

1

-

3

5

W sumie R u S krotka (1,2) występuje cztery razy (trzy razy z wystą w wielozbiorzc R i jedno z wiclozbioru .V), krotka (3, 4) występuje I i a krotka (5,6) tylko jeden ra/

Przecięcie R ^ Sjest z kolei następującym wielozbiorem:

li

2

4

Ą_

1

3