0225

226

III. Pochodne i różniczki

jeśli natomiast rozpatrywać kąty x<0,4129 (ss23°,5), to błąd będzie mniejszy nawet od 0,0001, itd.

Widzimy, że ze zwiększeniem liczby wyrazów wielomianu Taylora, wielomian ten z coraz większą dokładnością i w coraz większym przedziale odtwarza funkcję wyjściową.

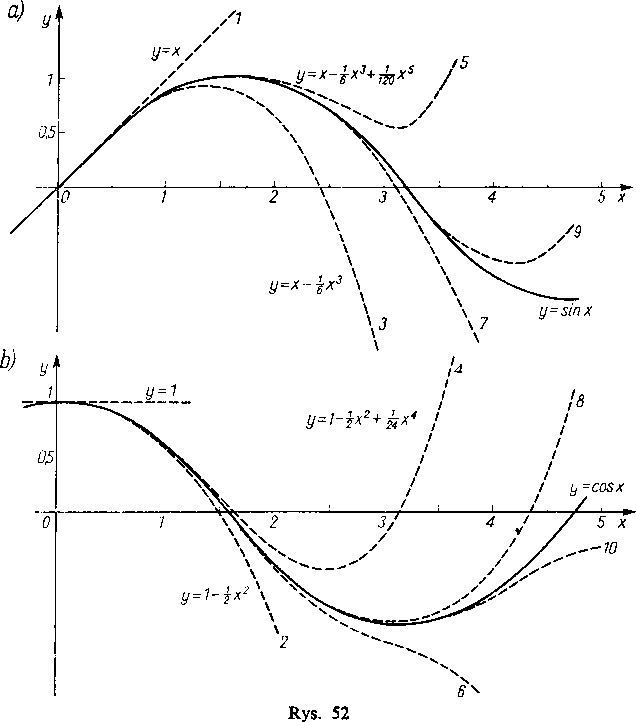
Ilustruje to poglądowo rys. 52a, gdzie obok funkcji y=sin x przedstawione są wykresy wielomianów

}' = x y = x—

x¹ x^s

y=x---1--,

6 120

itd.

1

Analogicznie dla /(x)=cos * mamy

*² x²    x^2m

2

cosx« 1---1---...+(— 1)---

2! 4!    (2m)!