0161

162

III. Pochodne i różniczki

Jeśli przyrost Ax nadany zmiennej x pociąga za sobą przyrost Ay dla y, to przez analogię do ustępu 90, za prędkość średnią zmiany y w porównaniu z x, przy zmianie x o wielkość Ax, można uważać stosunek

Ay

Wtedy prędkością zmiany y dla danej wartości x nazwiemy naturalnie granicę tego stosunku przy Ax dążącym do 0:

v= lim v_śr= lim — , a.x-*o    zix-oAx

tzn. właśnie pochodną y względem x.

W ustępie 91 rozpatrywaliśmy krzywą, określoną równaniem y—f{x), i rozwiązaliśmy zadanie konstrukcji stycznej do niej w danym punkcie. Obecnie możemy sformułować otrzymany wynik w sposób następujący:

Współczynnik kątowy tg a stycznej jest pochodną rzędnej y względem odciętej x.

Ta interpretacja geometryczna pochodnej bywa często pożyteczna.

Przytoczymy jako uzupełnienie do rozpatrzonych powyżej jeszcze kilka przykładów uwydatniających rolę pojęcia pochodnej.

Jeśli prędkość ruchu v nie jest stała i sama zmienia się z biegiem czasu t: v=f(t), to rozpatruje się prędkość zmiany prędkości nazywaną przyśpieszeniem.

Jeśli mianowicie przyrostowi czasu At odpowiada przyrost prędkości Av, to stosunek

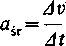
wyraża przyśpieszenie średnie w odcinku czasowym At, a granica jego daje przyśpieszenie ruchu w danej chwili:

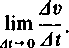
a= lim a_ir =

Jt-> o

W ten sposób przyśpieszenie jest pochodną prędkości względem czasu.

Zwrócimy się teraz do nauki o cieple i za pomocą pochodnej ustalimy pojęcie pojemności cieplnej ciała przy danej temperaturze.

Oznaczmy wchodzące do tego zagadnienia wielkości fizyczne w sposób następujący: 9 — temperatura (w stopniach C), W — ilość ciepła, której potrzeba, aby ogrzać ciało od 0° do 9° (w kaloriach). W jest oczywiście funkcją 6: W=f(9). Nadajmy temperaturze 6 pewien przyrost A6, wtedy W też otrzyma przyrost A W. Średnia pojemność cieplna przy nagrzewaniu od 9° do 9° + A9° będzie równa

AW

Je'

Ponieważ jednak przy zmianie A9 ta średnia pojemność cieplna na ogół się zmienia, nie możemy jej przyjąć za pojemność cieplną przy danej temperaturze 9. Aby otrzymać tę