0159

160

III. Pochodne i różniczki

Nadając odciętej x przyrost Ax, przejdziemy od punktu M krzywej do punktu M_x o odciętej x+Ax i rzędnej

y+Ay = a{x +Ax)²

(rys. 38a). Współczynnik kątowy tg ę siecznej MM, wyznaczymy z trójkąta prostokątnego MNM_X. Jego przyprostokątna MW jest równa przyrostowi odciętej Ax, a przyprostokątna

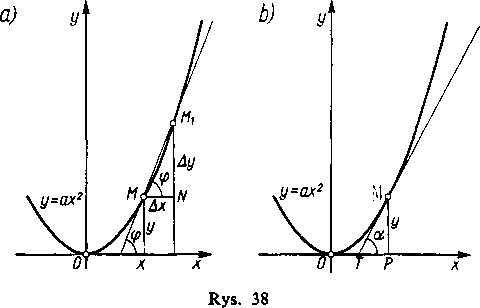
NM_X jest, rzecz jasna, odpowiednim przyrostem rzędnej

Ay = a (2 xAx + (Ax)²),

tak więc

tg <P =

Ay

Ax

= 2 ax + aAx.

Aby znaleźć współczynnik kątowy stycznej, trzeba, rzecz zrozumiała, przejść do granicy przy Ax-+0. Otrzymujemy w ten sposób wynik

tga= lim(2ax + azfx)=2ax. a*->o

Zauważymy przy sposobności, że wynika stąd wygodny sposób faktycznej konstrukcji stycznej do paraboli. Mianowicie w trójkącie MPT (rys. 38b):

y ax² x tg a— 2ax 2 ’

T jest więc środkiem odcinka OP. Tak więc w celu otrzymania stycznej do paraboli w jej punkcie M, wystarczy podzielić odcinek OP na połowy i środek jego połączyć z punktem M. W przypadku dowolnej krzywej o równaniu