0167

168

III. Pochodne i różniczki

2) w punkcie x₀ ma skończoną i różną od zera pochodną f'(x₀).

Wówczas w odpowiednim punkcie y₀=f (x₀) istnieje także pochodna funkcji odwrotnej g(y) i jest równa 1 lf'(x₀).

Dowód. Nadajmy wartości y=y₀ dowolny przyrost Ay. Wtedy funkcja x=g(y) uzyska odpowiedni przyrost Ax. Zwracamy uwagę na to, że jeśli Ay^O, to wobec jednoznaczności samej funkcji y=f(x) także i Axjt 0. Otrzymujemy

Ax 1 Ay Ay '

Ax

Jeśli teraz Ay-*0 w dowolny sposób, to na mocy założenia, że funkcja x=g(y) jest ciągła, również Ax-*0. Ale wtedy mianownik po prawej stronie równości dąży do granicy

f'(xo)/O i co za tym idzie, istnieje granica lewej strony równa odwrotności l/f'(x₀); ta granica jest właśnie pochodną g'(y₀).

Tak więc mamy prosty wzór

, 1

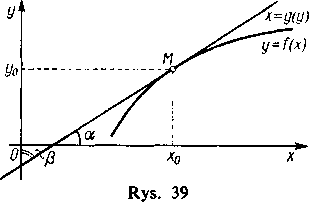
Łatwo jest wyjaśnić jego sens geometryczny. Wiemy, że pochodna jest tangensem kąta a utworzonego przez styczną do wykresu funkcji y=f(x) i oś x. Ale funkcja odwrotna x—g(y) ma ten sam wykres, tylko że zmienną niezależną odczytujemy dla niej na osi y. Wobec tego pochodna x'_y równa się tangensowi kąta P, który tworzy ta sama styczna z osią y (rys. 39). W ten sposób wyprowadzony wzór sprowadza się do znanego związku

tg a

tg/*=

między tangensami kątów a i /?, których suma równa się in.

Weźmy na przykład funkcję y=ef. Funkcją odwrotną względem niej jest x=log_ay. Ponieważ (patrz 6°) y'_x=a^K łn a, na podstawie naszego wzoru będzie

' = -1=    ¹ _^lQg°^e

^ y'_x a^x\n a y

co jest zgodne z 7°.

Przechodząc teraz do obliczenia pochodnych funkcji kołowych zmienimy dla wygody role zmiennych x i y, przepisując udowodniony wzór w postaci