0223

224

III. Pochodne i różniczki

Jeśli przenieść tu wyraz /(x₀) na lewo, to łatwo dostrzec, że wzór ten jest uogólnieniem wzoru Lagrange’a [112], który można napisać tak

/(*) ~f(xo) —/ (c) (x - x₀).

Chociaż najchętniej korzysta się właśnie z reszty w postaci Lagrange’a (ze względu na jej prostotę), w poszczególnych przypadkach jednak postać ta nie nadaje się dla oszacowania reszty. Trzeba wówczas korzystać z innych, mniej prostych, postaci reszty. Wymienimy tu jedną z nich — postać Cauchy'ego

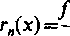
⁽ⁿ+¹⁾((x_o + 0(x~x_o)) n !

(i-mx-x₀y⁺¹,

którą otrzymujemy ze wzoru ogólnego Schlomilcha-Roche’a dla p= 1.

127. Wzory przybliżone. Dla uproszczenia przyjmiemy we wzorze (13) x_o=0, a zamiast c będziemy pisali 6x, gdzie 0<6< 1:

(14)

112!    n!    ' (n +1)!

Jeśli odrzucimy tu resztę, to otrzymamy wzór przybliżony

,, , ,/'(0) ,/"(0) _2i    ,/^(B)(0) ,

/(x)»/(0) + -_T-_r- x+ . x +...-I--— x

1 !

2!

Wzór ten zastępuje funkcję o charakterze skomplikowanym przez wielomian. Teraz jednak jesteśmy już w stanie oszacować błąd tego wzoru, równa się on bowiem co do wartości bezwzględnej właśnie odrzuconej reszcie. Jeśli na przykład pochodna rzędu n+1 jest ograniczona co do wartości bezwzględnej liczbą M (przynajmniej wtedy, gdy argument zmienia się między 0 a x), to

Mx”⁺¹ (n + 1)! ’

Rozpatrzymy kilka przykładów dotyczących funkcji elementarnych. Nie ma potrzeby powtarzać obliczeń z ustępu 125, będziemy tylko pisali w nowej postaci resztę.

1) Niech /(x)=e^x. Wzór przybliżony będzie

xx    x

:1 + —+ — +...+ -

1 ! 2!

n !

i ’

ponieważ reszta jest tu równa

„8*

r_n(x) =

„n+1

(n + 1)!