Untitled Scanned 02 (16)

1. CIĄGI

CZĘSC TEORETYCZNA

OZNACZENIA

(<i_n) - ciąg. którego wyrazami są liczby u,. a >. (h.....

<=> a_n - /i-ty wyraz ciągu (r/„i. np. a, - trzeci wyraz ciągu («„).

MONOTONICZNOŚĆ CIĄGU

Ciąg (ri„)jesł rosnący wtedy i tylko wtedy, gdy dla każdego neN, spełniona jest nierówność a_n, >a„ (czyli rt_/l+|-«_fl>0). Ciąg (a„) jest malejący wtedy i tylko wtedy, gdy dla każdego N, spełniona jest nierówność <a_n (czyli a,_l+|-n_;l<0 ).

CIĄG ARYTMETYCZNY

Ciąg («„) nazywamy ciągiem arytmetycznym wtedy i tylko wtedy, gdy istnieje taka liczba r. że a_n +, - a_n = r dla każdej liczby ne C,. Liczbę r nazywamy różnicą ciągu arytmetycznego.    *

<=> Wzór na n-ty wyraz ciągu arytmetycznego wi„): a„ = </, + (n - I )r.

Związek między trzema kolejnymi wyrazami ciągu arytmetycznego    ¹    .

CIĄG GEOMETRYCZNY

=*• Ciąg («„) nazywamy ciągiem geometrycznym wtedy i tylko wtedy, gdy istnieje taka liczba q, że a„ +\=a„q dla każdej liczby /i 6 (!,. Liczbę q nazywamy ilorazem ciągu geometrycznego.

=*> Wzór na n-ty wyraz ciągu geometrycznego («„): a_n=a^q^r'~\

I _ n

<=> Suma n początkowych wyrazów ciągu geometrycznego («,,): S„=a, —-—. gdy q * 1 i S„ = na,, gdy ą-1.

1-9

Związek między trzema kolejnymi wyrazami ciągu geometrycznego («„): a; =a„ ,

PROCENT SKŁADANY

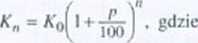
Kapitał A',, po n okresach kapitalizacji wyraża się wzorem

A',)- kapitał początkowy, p^c/r - stopa procentowa (taka sama w każdym okresie). n - liczba okresów kapitalizacji (miesięcy, kwartałów, lat itp.).

ZADANIA WPROWADZAJĄCE

Zdający potrafi • wyznaczać wyrazy ciągu określonego wzorem ogólnym

1.1 Wyznacz trzy początkowe wyrazy ciągu (a,,) o wyrazie ogólnym

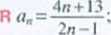
d) a_a=(-\f n:

c) a_n=/ł(/i—I )(/i—2)(/i—3); f) R a„= l^: + 2²+ ...+/i².

1.2 fl Sprawdź, czy istnieją takie wyrazy ciągu (/>.,) o wyrazie ogólnym b„ = 2n^{: l})n + 11. ktiSre są równe 7.