Zagadnienia semIV

MATEMATYKA NUMER PROGRAMU DKOS - 5002 - 54/04 PODSTAWOWY

ZAOCZNE UZUPEŁNIAJĄCE LICEUM OGÓLNOKSZTAŁCĄCE

SEMESTR IV

PYTANIA EGZAMINACYJNE............................

Pieczątka szkoły

2. Oblicz

1. Oblicz

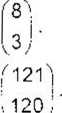
3. Oblicz

5 Wyrażenie 5I-6-7 zapisz w prostszej postaci.

6.    Ile liczb czterocyfrowych można zapisać z cyfr 1,2, 3, 4? Cyfry mogą się powtarzać.

7.    Ile jest permutacji zbioru pięcioelementowego?

8.    Ile jest dwuelementowych kombinacji zbioru dziesięcioelementowego?

9.    Ile jest dwuelementowych wariacji bez powtórzeń zbioru {1, 2, 3, 4, 5}?

10.    Ile jest dwuelementowych wariacji z powtórzeniami zbioru {1, 2, 3, 4, 5}?

11.    Ze zbioru liczb {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} wybieramy jednocześnie dwie. Określ zbiór zdarzeń elementarnych tego doświadczenia i oblicz jego moc.

12.    Ze zbioru kul ponumerowanych od 1 do 10 losujemy jedną, zapisujemy jej numer i odkładamy ją z powrotem. Czynność tę powtarzamy trzy razy. Określ zbiór zdarzeń elementarnych tego doświadczenia i oblicz jego moc.

13.    Z talii 52 kart losujemy kolejno 5 kart (bez zwracania). Określ zbiór zdarzeń elementarnych tego doświadczenia i oblicz jego moc.

14.    Z talii 52 kart losujemy kolejno 5 kart odkładając wylosowaną kartę do talii przed wyciągnięciem następnej. Określ zbiór zdarzeń elementarnych tego doświadczenia i oblicz jego moc.

15.    Rzucamy trzy razy monetą, a w przypadku, gdy otrzymamy trzy razy ten sam wynik rzucamy po raz czwarty. Określ zbiór zdarzeń elementarnych tego doświadczenia i oblicz jego moc.

16.    W urnie znajdują się 4 kule białe i 3 czarne. Rzucamy monetą. Gdy wypadnie orzeł, to losujemy jedną kulę z urny, gdy wypadnie reszka, losujemy 2 kule. Określ zbiór zdarzeń elementarnych tego doświadczenia.

17.    Na stole stoją dwa pojemniki. W pierwszym jest sześć kul białych i pięć czarnych, w drugim cztery białe i pięć czarnych. Z losowo wybranego pojemnika losujemy jedną kulę. Określ zbiór zdarzeń elementarnych tego doświadczenia.

18.    Rzucamy trzy razy symetryczną kostką do gry. Oblicz prawdopodobieństwo otrzymania co najmniej raz nieparzystej liczby oczek.

19.    Rzucamy trzy razy symetryczną kostką do gry. Oblicz prawdopodobieństwo otrzymania co najmniej raz sześciu oczek.

20.    Rzucamy trzy razy symetryczną kostką do gry. Oblicz prawdopodobieństwo otrzymania co najmniej raz sześciu oczek i co najmniej raz nieparzystej liczby oczek.

21.    Ze zbioru {1, 2, ..., 9} losujemy kolejno trzy razy po jednej cyfrze bez zwracania i zapisujemy wylosowane cyfry w kolejności losowania. Otrzymujemy liczbę trzycyfrową. Oblicz prawdopodobieństwa otrzymania liczby podzielnej przez 5.

22.    Ze zbioru {1, 2,    9} losujemy kolejno trzy razy po jednej cyfrze bez zwracania

i zapisujemy wylosowane cyfry w kolejności losowania. Otrzymujemy liczbę trzycyfrową. Oblicz prawdopodobieństwa otrzymania liczby parzystej.

23.    Z pudełka, w którym jest 12 kul białych, 9 kul zielonych i 6 kul niebieskich wylosowano kolejno , bez zwracania, dwie kule. Sporządź drzewko stochastyczne.

24.    IZ pudełka, w którym jest 12 kul białych, 9 kul zielonych i 6 kul niebieskich wylosowano kolejno , bez zwracania, dwie kule. oblicz prawdopodobieństwo zdarzenia, że za drugim razem wylosowano kulę niebieską.

1