Untitled Scanned 17 (9)

a następnie sprawdzamy dwa dalsze warunki:

£ X= +417-417=0;

£ Y= +1910 + 3090-2000-3000=0.

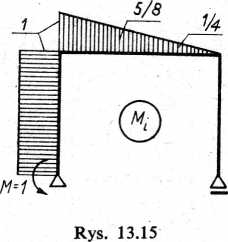
Kontrola zgodności przesunięcia (por. p. 13.4.4). Obliczmy kąt obrotu przekroju podporowego A; wiemy, że w rzeczywistości musi on być równy zeru. W tym celu obciążamy układ w miejscu i na kierunku poszukiwanego przemieszczenia siłą uogólnioną (momentem) równą (równym) jedności i sporządzamy wykres momentów jednostkowych M_t (rys. 13.15). Kąt obrotu obliczymy wg wzoru (13.10) wykorzystując sposób Wereszczagina:

„ r mm _t 1

Ponieważ wykres M na rys. 13.13 1 jest sumą wykresów z rys. 13.13e,f, k, j, wobec tego przy całkowaniu skorzystamy właśnie z tych wykresów:

,. = l.l-3(3000 ₊ 9000) _{+ 2}-l₇({

1 500+

1

⁺r³

9000

1

3

T

i

3000 + —- 3-4500+ 4

3-12350-1 —

EJ    2 EJ 2

2 1 1

4-12350--- 1+----3-1250-1 +

3    EJ 2

+-i-•-i-• 1 ■ 4 • 1 250 = — (45190 - 45 200) » 0. 2EJ 2    EJ

Błąd wynosi w tym przypadku (wzór 13.20):

100 = 0,02%.

45200-45190

45190

Widzimy więc, że warunek zgodności przemieszczeń jest spełniony, a kąt obrotu przekroju na podporze utwierdzonej równy jest zeru-

Przykład 13.2. Obliczyć nadliczbowe wielkości statyczne w ramie symetrycznej obciążonej anty-lymetrycznie (rys. 13.16a). Przyjmujemy schemat podstawowy jak na rys. 13.16b. Następnie sporządzamy wykresy momentów od sił jednostkowych i od obciążenia zewnętrznego (rys. 13.16c+f).

Układ równań kanonicznych metody sił określających przemieszczenia na kierunkach poszukiwanych niewiadomych przybiera postać:

455