P1010771

174 3. FUNDAMENTY 33. WYMIAROWANIE STOF FUNDAMENTOWYCH 175

174 3. FUNDAMENTY 33. WYMIAROWANIE STOF FUNDAMENTOWYCH 175

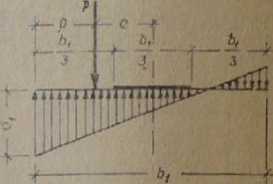
Rys. 3.14. Działanie siły pionowej poza rdzeniem podstawy fundamentowej

(3.32)

-o,— ■

(3.33)

ziemią można w pierwszym

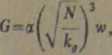
(3.35)

(3.37)

a,m

(3.39).

dla przypadku jak na rys. 3.11 otrzymamy

*„2L£+2*.    M

p p

Wysokość stopy określa się tu jak pety obciążeniu osiowym. Przy obliczaniu ekonomicznej wysokości stopy można korzystać z tab. 3.3 odczytując współczynnik k w zależności od dopuszczalnych naprężeń na grunt k_t, przy czym wzór ma postać

/i=K(d₁+2e-«_iI).    (3.29)

Jeżeli stopę fundamentową zaprojektuje się tak, by środek jej podstawy pokrywał się 7. osią działania siły P, to znaczy by mimośród c równy był zeru, to wykres oddziaływania gruntu na podstawę będzie miał kształt prostokąta. Wtedy dalszy ciąg obliczeń przeprowadza się jak dla stopy obciążonej tylko siłą osiową. Przypadek ten rozpatrzono w przykładzie 20. Gdy nie można nadać stopie takiego kształtu, aby uniknąć mimośrodu siły P, a może to mieć miejsce przy zmiennych wielkościach układa sił działających na stopę, wtedy wykres odporu gruntu będzie trapezowy lub trójkątny. W tym przypadku

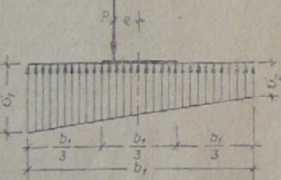
Rys. 3.13. Działanie siły pionowej w rdzeniu podstawy fundamentowej

skrajne naprężenia pod krawędziami stopy przy liniowym ich rozkładzie oblicza się według wzorów dla mimośrodowego ściskania; ewentualne naprężenia rozciągające pod stopą pomija się w obliczeniach. W związku z powyższym rozróżnia się tu dwa przypadki.

1. Gdy P-N+G działa na mimośrodzie e^bJ6 względem środka podstawy stopy wtedy otrzymamy ekstremalne wielkości naprężeń na grunt

Z+HLZ.I	hi a	(3.30)
p w Ęm
PM P |	f'--V	(3.31)

Przy założeniu, że N i G działają w jednej osi, odpór gruntu obliczamy według wzorów ___i G

W

G

Mi

Ciężar własny fundamentu wraz ze spoczywającą na nim przybliżeniu przyjąć

(3.34)

gdzie a«=l,2-rl,5 N w tonach, k_t w T/m¹; głębokość posadowienia w w metrach.

Po przyjęciu wymiarów stopy fundamentowej można przeprowadzić korektę jej ciężaru, dla stopy piramidalnej ciężar bryły fundamentowej wynosi: dla stopy o podstawie kwadratowej, rys. 3.16

> C=y|^6^Jd+^j^(6^ł+ha+fl^J)J, dla stopy o podstawie prostokątnej, rys. 3.15

G=₇|b_I6_Jd+^[(2h₁+o₁)h₂+(2a_J+6_J)fl_J]J.    (3.36)

gdzie y — ciężar objętościowy materiału stopy.

Sprawdzenie wg wzorów (3.35) i (3.36) ma uzasadnienie w przypadku mimośrodowego obciążenia stopy, gdyż dla ściskania osiowego założone wymiary stopy wg wzoru (3.9) są zazwyczaj miarodajne.

2. Gdy P^N+G działa na mimośrodzie e>bj6 względem środka podstawy stopy, wtedy otrzymamy maksymalne naprężenia krawędziowe

2P

Wm

W tym przypadku część podstawy fundamentu nie bierze udziału w przekazywaniu ciśnień na grunt. Zjawisko takie można dopuścić tylko pod słupami obciążonymi momentami wywoływanymi obciążeniem zmiennym z wyjątkiem obciążeń dynamicznych. W szczególności odrywanie można dopuścić tylko wówczas, gdy podstawa fundamentu jest położona powyżej zwierciadła wód gruntowych, przy tym musi być spełniony warunek

-^2*0,75.    (3.38)

Przy nieuwzględnianiu rozciągania w gruncie pod stopą będzie <Tj=0. Przy założeniu jak w przypadku 1 odpór gruntu obliczamy według wzoru

G

IR

Mając obliczone wartości odporu gruntu, oblicza się momenty i zbrojenie dla poszczególnych kierunków stopy fundamentowej w podobny sposób jak przy stopach obciążonych osiowo. W przypadku trapezowego lub trójkątnego wykresu odporu gruntu w kierunku działania momentu zbrojenia dla stopy, należy obliczyć dla tego wspornika, na który działa większy odpór gruntu. Zbrojenie dla kierunku prostopadłego oblicza się na moment spowodowany odporem gruntu na jeden z trapezów, prostopadle usytuowany do płaszczyzny działania momentu w podstawie stopy.