75086 P1010778

188 3 FUNDAMENTY

Przy założeniu odpowiedniej sztywności fundamentu ławowego bądź płytowego można obliczenie momentów i sił poprzecznych przeprowadzić również jak dla belek przewieszonych jedno- lub wieloprzęsłowych. Ważną też rolę przy wyborze metody obliczania pasm fundamentowych odgrywa sztywność konstrukcji przekazującej obciążenie na fundament, Poza tym należy przestrzegać, aby wypadkowa sił przekazywana przez podpory przechodziła przez środek ciężkości pasma fundamentowego oraz aby reakcje fundamentu pokrywały się z siłami przekazywanymi przez podpory.

3.5.1. Ławy fundamentowe pod dwoma słupami

Długość ławy określamy z warunku

M

(3.53)

gdzie j_k - średni ciężar ławy fundamentowej wraz z ziemią na niej spoczywającą, w - głębokość posadowienia fundamentu, b - szerokość ławy, k_t - dopuszczalne naprężenie na gnrnh

	ł— —Ą— K, 1 i i	*
■	I _i_	■
_ Ol i__ ‘i W 1		. __
l
_ł!_o		2

Rys. 3.24. Schemat statyczny fundamenta o nucie ftoiiokątiym pod dwom* słupami

i i l firn i;n 11 t^grrrr

tfr

I. W przypadku n,s=n₃=n oraz W,*/i₂₎ otrzymamy wartości momentów wspornikowych ze wzorów

w

<3.35)

mm

moment pnęsłowy jak dla belki przewieszonej z dwoma wspornikami

¹²    8    2 ^m2[ 4 J’

przy czym    " odpór gruntu.

2. W przypadku <r,*fl₂ oraz N,*N₂, zaś b=const

(3.56)

1    , Ę

2    1-fc

(3.57)

Ćip

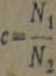
(3.58)

Moment przęslowy M_n oblicza się jak dla belki jednopizęslowej z dwoma wspornikami.

3. W przypadku    przyjmując a_x^a_u otrzymamy fundament w rzucie nie

prostokątny, lecz trapezowy.

Rys. 325. Schemat statyczny fundamentu o rzucie trapezowym pod dwoma stupami

Wzory na obliczanie szerokości lawy i momentów wspornikowych przyjmą postać

_N_xe_x+N₂e₁ I ^£=' W ‘2’

	. / 6e\
avbxa^2	P isH
2 '	«a 2

(3.59)

(3.60)

(3.61)

Momenty przęsłowe M_xi Obliczamy jak w przypadku 2