Image13 (38)

80 Rozwiązania zadań ze zbioru "MENDLA

Pa • I - Pa • b + b • g • p • I - b² • p • g = Pa ■ I - Pa • bi - bi • p • g • I + b? • p. g

-    b? • p • g + Pa • bi    + bi • p • g •    I +    b • (Pa + P    •    g • I - b • p •    g) = 0

-    p • g • b? + (p_a + p    • g • I) • bi + b •    (p_a + p • g    •    I - b ■ p • g) = O

A = (Pa 4- p ■ g • l)² +    4 • p • g • b •    (p_a + p • g • I    -    b • p • g)

Va = V(pa + p • g • \    + 4 • p • g •    b •    (p_a + p • g    •    I - b • p • g)_

- (pi + p . g . I) + V(p_a + p- g-l)² + 4- p- g- b-(p_a + p- g- l- b- pTg

¹    _ ~ ² • P ■ g_

_ pi + p • g • I - V(p_a + p • g • I)² + 4 • p • g • b (p_a + p • g • I - b • p • g)~

¹    _² • P • 9__

P1 + p • g • I + V(p_a + P • g • I)² + 4 • p • g • b • (p_a + p • g • I - b • p • g)~ ^b2=    2-pg    ^>b

b2 > b nie spełnia warunków zadania.

Po podstawieniu danych i wykonaniu prostych obliczeń otrzymamy bi « 1,8cm

Odp.: W rurce zostanie słupek rtęci o długości 1,8 cm.

Zadanie 592 str.119

Szukane:

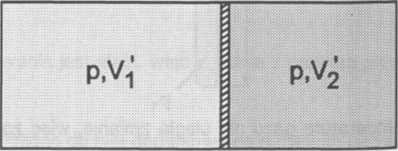
P, Vi‘, V₂‘

Dane:

Pi, p2> Vi, V2

Po odblokowaniu tłoka przesunie się on tak, że ciśnienie w obu częściach cylindra będą jednakowe.

Temperatury gazów są stałe, więc gazy zostały poddane przemianie izotermicznej.

Dla pierwszej części cylindra otrzymamy:

pi • Vi = p • vr —)

Dla drugiej części otrzymamy:

P2 • V2 = p • V2' —^

P1-^v1	P2.V2

Vi' =

pi-Vi

P

V₂' =

P2-V2

P

Wymiary cylindra są stałe, więc objętość całego cylindra przed i po odblokowaniu tłoka będzie taka sama.

Stąd Vi + V2 = Vi' + V₂'

Po podstawieniu odpowiednich wyrażeń za V‘i i V‘2 mamy:

w w Pi • Vi P2 • V2

Vi + V₂ = ^r-— + --    /• p

P    P

Przekształcając ostatnie równanie wyznaczymy końcowe ciśnienie, p • (Vi + V2) = pi • Vi + p2 • V₂ /: (Vi + V2)

Pi • Vi + P2 • V2 ^P Vi + V₂

Mając p obliczymy objętość obu części gazu.

V1' =

P1 • V1

p1 • Vl + P2 • V2 V1 +v₂

_V|,_Pi • Vj • (Vi + Vż)

p1 • Vl + P2 • V₂ P2 • V2

V₂' =

V₂' =

p2 • V2

P1 • Vl + P2 • V2 V1 +v₂

w / _ p2 • V2 • (Vl + V2)

² pi • Vi + p₂ • v₂

^0dP-^: Po odblokowaniu tłoka ciśnienie w obu częściach cylindra ma war-P1 • Vi + p₂ • V₂

tość p = -—y-~y₂-, a objętości obu części cylindra będą:

V_1> = P¹ Vj .₍v, ₊ v_a) oraz v P2 V2 (V_{1 +} V₂)

P1 Vl+P2 V2    pi*Vi+p₂ V₂

Dane:

V,’    P3.

^V,'^V2,V₃

Zad.593    str.119

Szukane:

p = ?

Vi‘, V₂‘, v₃‘ = ?