Image10 (41)

109 Rozwiązania zadań ze zbioru "MENDLA

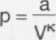
Wyznaczone p podstawimy do równania p V = n-R-T.

Stąd — V = n-R-T V^K

Po przekształceniu:

a ■ V¹ “^K = n • R • T /: a

a-T

_Vi-K_n- R

Pierwiastkujemy obustronnie otrzymane równanie.

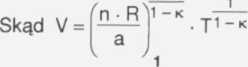
„ n • n ' -k

wyrażenie _g    jest stałe ponieważ n jest ilością moli gazu, R jest stałą

gazową i a jest również wielkością stałą. Oznaczymy tę stałą literą A, więc:

Ostatecznie otrzymamy zależność objętości V gazu od jego temperatury T

w postaci V = A • T¹ -«

Zadanie 617 str.124

Dane:

Vi = 6drrP pi =2-10⁶ Pa

Szukane:

P2 = ?

t₂ = ?

ti = 27°C stąd Ti = 273K + 27 K = 300K V₂ = Odm³ k= 1,4

Gaz poddano przemianie adiabatycznej, więc: pi • V? = p2 • V5 /: V5 V?

stąd P2 = Pi • —

p2 = 2-10⁶Pa • 2¹*⁴

p2 = 2-2^1,4 • 10⁶Pa = 2 -2,64 ■ 10^b Pa p2 - 5,28 • 10⁶ Pa = 5280000 Pa = 5280 kPa Znając ciśnienie p₂ możemy obliczyć T2 z równania gazu doskonałego.

pi • Vi _ P2 • V₂ Ti ' T₂

pi • Vi • T₂ = p2 • V₂ • Ti /: (pi • Vi)

T₂ =

, lecz

P₂ = Pi

P2 • V₂ • Tl P1 • V1

T₂ =

P1 •	f^v0	K • v2 • Tl
	V / P1	•Vi

fyiT

‘ V₂

V /

T l^Vl'

^{T2 = l}vi

t₂ =

T₂ =

Ii

Yi

v₂

vK-1

•Ti

^/6 dm³

■ 300K

3 dm³

\ /

T₂ = 2^0a ■ 300K= 1,32 -300K T₂ «396K

Odp.: Ciśnienie końcowe wynosi ok. 5,28 10⁶ Pa, a temperatura końcowa 396/C.

Dane:

Zadanie 618 str.124

Szukane:

Ap = ?

Pi-10⁶ Pa Vi = 2 m³ V₂ = 8 m³

Ap = P2-P3

P2 - ciśnienie gazu po przemianie izotermicznej P3 - ciśnienie gazu po przemianie adiabatycznej

Zgodnie z prawem przemiany izotermicznej