Image18 (30)

40 Rozwiązania zadań ze zbioru "MENDLA

S - pole przekroju cylindra

Z równania Clapeyrona gazu doskonałego dla obu części cylindra otrzymujemy:

pi • Vi rm ^

Ti ^=_R

oraz

p2 • V2 m2

• R

M-1    T2 M2

Z treści zadania wiemy, że masy gazu są jednakowe,mi = m2 i tłok dobrze przewodzi ciepło, więc Ti = T2 = T.

Układ ma być w równowadze, co oznacza, że: pi = P2 = P

Teraz możemy oba równania zapisać w postaci:

P- Vi _ m _R T m

m

p . V₂ = — • R T

P2

p = m • R •

/: V2

M-2 • V2

Wyznaczone ciśnienie p podstawiamy do równania Clapeyrona dla pierwszej części cylindra z tlenem:

m • R • —“tt” • Vi _P2 • V2 _ m _R

1    W

m • R ■ T • Vi 1 m „

-77-• = =—• R /: m • R

P2 • V2 T pi

Vi

_w = —    /• P2 • V2 • |A1

P2 • V2 m

Vi • P1 = V2 • H2

Vi = S • x    oraz

stąd S • x • pi = S • y • p2 /: S • pi

y • P2

lecz

V₂ = S • y

x =

Pi

Z rysunku można odczytać, że: x + y = I

Stąd, po podstawieniu x mamy:

—— + y = i /• 1x1

w

y • M2 + m • y = m • l

Po przekształceniu otrzymanej zależności otrzymamy odległość y tłoka od jed* nej ze ścian.

y •(P2 + P1) = P1-I /:(P2 + P1)

y =

P1 • I

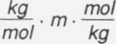
[y] =

[y] =¹⁷¹

0,032 • 0,85 ^y " 0,032 + 0,002 0,032 • 0,85 ^y"    0,034

y = 0,8 m

y = 80 cm,    ale    x = I — y

stąd x = 5 cm

Odp.: Tłok będzie znajdował się w odległości 5 cm od jednej ze ścian bocznych.

Zadanie 563 str.112

Dane:

V = 12 dni³ = 0,012 nt³ S = 0,6dm² = 0,006m² mi = 2g = 0,002 kg Ti = 300K

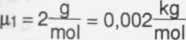
mi = 4g = 0,004kg T₂ = 280K

Szukane:

m = ? - masa tłoka

jednostki:

[y] =

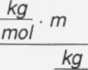
kg kg _ mol ^m mol mol ~ kg

mol

Q - ciężar tłoka

Pi - parcie wodoru na tłok

P2 - parcie helu na tłok

Układ jest w równowadze, więc: Pi = Q + P₂ /: S