Image27 (22)

52

gdzie cp — cp(t) jest nieznaną funkcją czasu. Różniczkując te równania czasu otrzymujemy

x = r (1 — cos (p) (p,

y

v — 2 r

r cp situp,

a stąd

. (p d(p sm - — 2 dt

Ograniczając się do jednego obrotu możemy opuścić znak bezwzględności

v — Lr sin — cp

2 *

Pozwoli nam to składowe prędkości wyrazić w postaci

. <P

x = v sin —

2 cp

) = V cos —.

2

Różniczkując składowe prędkości względem czasu i uwzględniając, że

v

<P = ->

2 r sm -

2

o trzy

II

ujemy składowe przyspieszenia

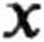
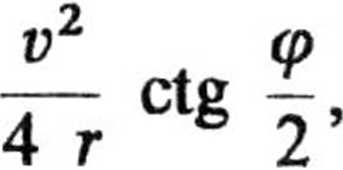
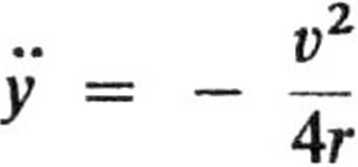
Ponieważ v = const, istnieje tylko przyspieszenie normalne

_A . <P p' 4r sm —

2

Stąd

i

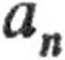
= 4r sin

<P

2

i

i

i .

<4.17* W biegunowym układzie współrzędnych wektory prędkości i przy spieszenia mają postać

V

r i_r + rep i_v,

a =

(r - rep¹) l +    + 2 rep) i ,

gdzie wektor jednostkowy i_r ma kierunek wektora wodzącego, a wektor jedno stkowy i₉ jest prostopadły do niego, o zwrocie zgodnym z przyrostem kąta cp Wstawiając do tych wzorów odpowiednie wartości, otrzymujemy

v = crT_r + brt ,

a

(c

b¹) ri_r + 2berty.

Kąt cl między tymi wektorami obliczamy za pomocą iloczynu skalarnego

v • a

cosoc =

yj v • v yj~a • a

y/C¹ + b¹

M8

a)    r — ct, cp = bt.

c

b)    ^r = - cp.

Jest to równanie spirali Archimedesa.

<P¹.

c) v — c \J1 -ł- b¹1¹ — c \/l^

d) a — bc y/4 + b¹1¹ = bc y/4 + cp¹

1