Strona0270

270

gdzie: col —— oraz    jest okresową funkcją czasu. Przyjmując z ko-

l    8

lei, że

s(t) = s_Q cos ćot    (11.3)

równanie (11.2) można przekształcić do postaci

q + co\ [l-26cosctf]ę> = 0    (11.4)

b)

• m

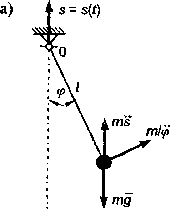
Rys. 11.1

Równanie (11.4), zwane równaniem Mathieu, oraz bardziej ogólne równanie (11.2), zwane równaniem Hilla, odgrywają zasadniczą rolą w teorii drgań parametrycznych. W technice występuje cały szereg ważnych praktycznie układów mechanicznych, w których mogą powstać drgania parametryczne. Można tu wymienić np. płaskie drgania giętne wałów wirujących o niekołowym przekroju, drgania mechanizmów korbowo-wodzikowych z kołem zamachowym i wiele innych.

11.2. Drgania parametryczne nietłumione

Zajęto się teraz zbadaniem równania Hilla jako ogólniejszego od równania Mathieu

x +®²[l-/(<)]* = 0    (11.5)

gdzie: f{t) - okresowa funkcja czasu.