img064 (6)

3

METODY ANALITYCZNEGO PRZEDSTAWIANIA SYGNAŁÓW Uogólniony szereg Fouriera (cd)

•    można udowodnić, że dowolną odcinkami ciągłą funkcję x(t), spełniającą warunek

h

J]x(f)(²^ < 00

h

można rozwinąć w szereg względem funkcji bazowych u₀(t), «>(/),...,

tworzących układ liniowo niezależnych funkcji ortogonalnych, tak, że ze wzrostem ich liczby (n ) błąd aproksymacji maleje

co

x(t)= a₀u₀(t)+ a_xu_x{t)+ a₂u₂(t)+... = £0,11, (f)

/=0

•    funkcja x(t) spełniająca powyższy warunek nazywa się funkcją całkowalną z kwadratem; wszystkie sygnały stosowane w elektronice są całkowalne z kwadratem, gdyż warunek ten oznacza, że energia sygnału wydzielana na jednostkowym obciążeniu jest skończona

•    zbiór funkcji w₀(/), «i(/).....w,(/),... spełniający w przedziale < /,,/₂ > warunek

h

)dt = O dla i ¹ j, gdzie ij = 1,2,...

'i

nazywa się układem funkcji ortogonalnych w przedziale ortogonalności < t_x,t₂ >

4

METODY ANALITYCZNEGO PRZEDSTAWIANIA SYGNAŁÓW Uogólniony szereg Fouriera (cd)

•    jeżeli ponadto zachodzi równość

]uf{t)dt=E_t = \,i = 1,2,... h

to układ nazywa się ortonormalnym (baza ortonormalna)

•    jeżeli dla danego układu funkcji E¹ 1 to układ ten można unormować mnożąc u[t) przez 1/JĘ

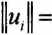
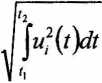
nazywa się normą sygnału

• układ funkcji u,(t\ i = 0,1,2,... nazywa się liniowo niezależnym, jeżeli żadna z funkcji tego układu nie może być wyrażona w postaci liniowej kombinacji pozostałych

1

wielkość