P1020151

(103)

Henryk Juszka

odpowiedzi liniowo-czasowej:

s

V(s) = k~,

hfl)

t

b)

k(t)

k

Rys. 27. Charakterystyki czasowe elementu całkującego idealnego: a) skokowa;

b) impulsowa

Idealne elementy całkujące w rzeczywistości nie występują, ponieważ wszystkie elementy urządzeń mają pewną masę i cechują się w związku z tym pewną inercyjnością ruchu. Dlatego elemjenty całkujące, spotykane w praktyce technicznej, nazywa się rzeczywistymi elementami całkującymi i tylko niekiedy -przy małych inercjach można je przybliżyć za pomocą idealnych.

Element całkujący z inercją (rzeczywisty)

Realizowany jest jako szeregowe połączenie członów całkującego idealnego i inercyjnego. Ze względu na praktyczne znaczenie został przedstawiony poniżej (rys. 28). Transmitancja tego elementu jest następująca:

G(s) =

k

1

s(l+sr) ! j7)(1+jD

(104)

Odpowiedzi czasowe rzeczywistego elementu całkującego dla standardowych wymuszeń:

— skokowego:

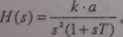
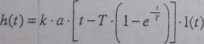
impulsowego:

_K,_a).    * -    *(*) - * o - «** m    oof|

s(l + sT)

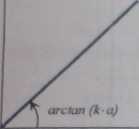
liniowo-czasowego:

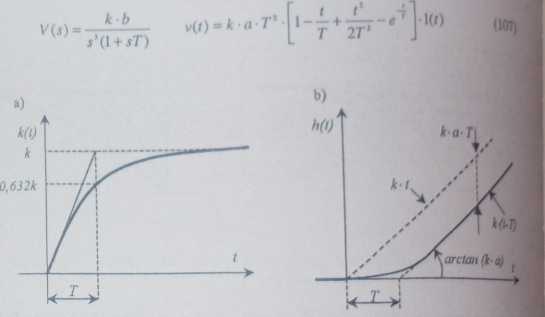
Rys. 28. Charakterystyki czasowe elementu całkującego rzeczywisty: a) impulsowa; b) skokowa

Człon różniczkujący idealny D (differentiation)

Jest to element, w którym wielkość wyjściowa jest proporcjonglH pochodnej wielkości wejściowej. Równanie transmitancji układu jest następują^

G(s) = sk = sT_D    (108,

gdzie: Ta - czas różniczkowania.

W członie różniczkującym idealnym sygnał wyjściowy jest proporcjoMiĘm do pochodnej sygnału wejściowego wzglądem czasu. Ponieważ stopień IkflH transmitancji jest wyższy od stopnia mianownika, człon ten jest niemożliwą! zrealizowania w praktyce i może być modelowany jedynie w przybliżeniaCffl rakterystyki tego elementu przedstawiono na rys. 29. Odpowiedzi na wymuszeni* 1