P1020820

E

O.

X

0    50 100 150 200 250

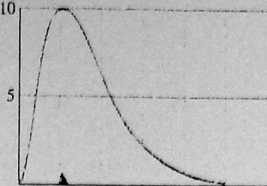
odległość [pm]

Rys. 40.18. Rozkład radialnej gęstości prawdopodobieństwa P(r) dla stanu podstawowego atomu wodoru. Trójkąt został umieszczony w odległości jednego promienia Bohra od początku układu współrzędnych. Początek układu współrzędnych oznacza środek atomu

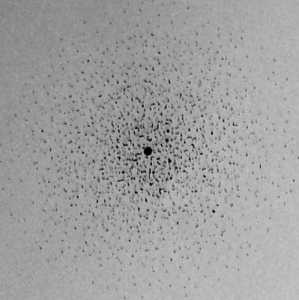
Rys. 40.19. Rozkład gęstości prawdopodobieństwa \łr²(ję)» a nie radialnej gęstości prawdopodobieństwa P{r) dla stanu podstawowego atomu wodoru. Gęstość kropek maleje wykładniczo ze wzrostem odległości od jądra, które jest tu oznaczone czerwonym punktem. Wykresy takie mogą pomóc w wyobrażeniu sobie „chmury elektronowej” atomu

Tabela 40.3. Liczby kwantowe stanów atomu wodoru o liczbie kwantowej n = 2

n	l
2	0	Q
2	1	ii
2	1	0
2	1

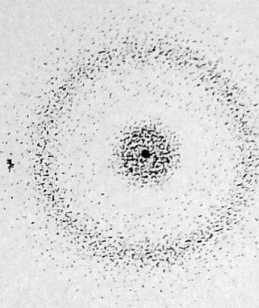
Rys. 40.20. Rozkład gęstości prawdopodobieństwa ^²(r) dla atomu wodoru w stanie o liczbach kwantowych n = 2. I = 0 i m/ = 0. Rozkład ma symetrię sferyczną, a środkiem symetrii jest jądro. Pusty pierścień widoczny na rysunku odpowiada sferze, na której gęstość prawdopodobieństwa \k²(r) = 0

, -

mi = 0

a)

• •* i*'-* * V

mmm

mm

m_t = ±1

b)

Rys. 40.22. Rozkłady gęstości prawdopodobieństwa \f/²(r,6) dla atomu wodoru w stanach o liczbach kwantowych n = 2, l = 1. a) Rozkład dla stanu o liczbie kwantowej m/ = 0. b) Rozkład dla stanów o liczbach kwantowych mi = -fl [mi = —1. Oba rozkłady pokazują, źe gęstość prawdopodobieństwa ma symetrię osiową, a osią symetrii jest oś z

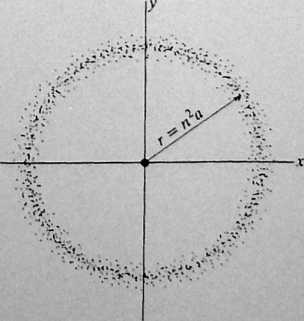
Rys. 40.23. Rozkład radialnej gęstości prawdopodobieństwa P(r) dla atomu wodoru w stanie kwantowym o stosunkowo dużej głównej liczbie kwantowej w = 45 i orbitalnej liczbie kwantowej l n — \ = 44. Kropki znajdują się w pobliżu płaszczyzny .ty, pierścień kropek zaś sugeruje istnienie klasycznej orbity elektronowej