P1080224

4. Wprowadzenie do kinematyki robotów

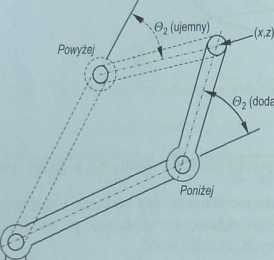
o dwóch ramionach są możliwe dwa sposoby osiągnięcia punktu o współ-1 rzędnych x, z- rys. 4.10. Można je uzyskać przez sterowanie robota. Dla przy-1 kładu, w języku programowania mogą występować komendy Powyżej i PoniżejM które określają, czy w przegubie między ramionami ma nastąpić obrót o kąt 6M w kierunku ujemnym lub dodatnim. W pokazanym na rys. 4.10 przykładzie I przyjmijmy kąt 0₂ za dodatni.

&₂ (dodatni)

Rysunek    _____ ■___

Dwa możliwe położenia ramion robota do osiągnięcia pozycji efektorai-W punkcie o współrzędnych z, z

Za pomocą tożsamości trygonometrycznych cos (,4 + B) = cosA cosjB - siki sinB

sin (A + B) = sin/4 cos B + sinficos./4 ■"    __s;c;    (4.18)

wzory (4.16) i (4.17) można przedstawić w postaci x=/icos0j + /₂cos0|Cos0₂ - /₂sin0isin02

z = /isin<9j + /₂sin0|Cos02+ /₂cos0isin0₂

Po podniesieniu do kwadratu obu stron tych równań i dodaniu otrzymuje się

(4.20)

Po zdefiniowaniu kątów a i j| (rys. 4.11) można napisać h sin 02

94

(4.19)

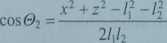
/₂ COS0₂ +1\

tgf = -x

(4.21)

> strukturę szeregowej

4.2. Kinematyka robotów o

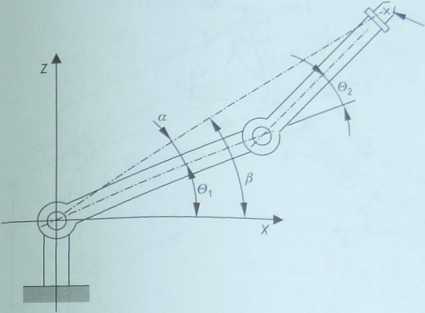
Rysunek    ___

Ilustracja oznaczenia kątów a i p

Z tożsamości trygonometrycznej

tg (A-B) =

tg A —tg B 1 + tgAtgB

(4.22)

otrzymuje się

tg 0i jg

z(li + h cos &2 ) ~ xh sin 0₂ x{l\ +/₂ cos 02) +2/2 sin 02

(4.23)

Znając długości ramion l\ i /₂, można obliczyć potrzebne kąty, które umożliwią umieszczenie efektora w zadanym punkcie o współrzędnych x, z w przestrzeni.

4.2.3.3. Robot o trzech stopniach swobody w przestrzeni o dwóch wymiarach

Robot o dwóch ramionach ma bardzo małe zastosowanie praktyczne. Przez dodanie trzeciego stopnia swobody otrzymuje się robota {B_R1, B_R2, B_m} - rys. 4.12. Ten trzeci stopień swobody to przegub nadgarstkowy. Ma on większe możliwości orientowania się w przestrzeni i ustawienia narzędzia.