P3041028

n 7 Projektowani* słupów ram parterowych

n 7 Projektowani* słupów ram parterowych

0,5 7,5 1.1 = 4,2 kN 0.12 6.0 7.5 1.2 - 6,5 kN 0.2 6,0 4 1.1 = 5,3 kN 1,68 54.0 0,8 * 72,6 kN (24,0 + 45 0,5) '1,10,9* 46.0 kN

ciężar własny słupa

188,6 kN ± 3,5 kN

ścianka z przykł.5.11 rygle z przykładu 5.11 śnieg z przykł 2.1. poz.2.1.2 udźwig z poz.2.13 Razem wtatT

3. Najniekorzystniejsze obciążenie słupów — słup nawietrzny (lewy)

N_f = 188.6 3,5105.1 kN, M = 71,0 kNm — słup zawietrzny (prawy)

Wc = 188.6 + 3.5 = 192,1 kN, M=42,1 kNm

4.    Dobór przekroju poprzecznego słupa Przekrój dobrano metodą 'próby”:

^A=s>^Hji^s30cm

Przyjęto I 300. 4 = 69.1 cm². W*=653 cm³. i_y= 2,56 cm, /_x = 11.9 cm ŚcianKi przekroju są klasy 1.

5.    Wymiarowanie

Nośność słupa sprawdzono wg wzorów (6.3), (6.4):

N $xMx , i*

9« Nfle «PL Mrk

A,= 1.25„,* _s0.1 Mrx Nrc

Nośność obliczeniowa przekrojów

Nfic = 69.1 20,5 = 1416,5 kN

Mn* = 1.07 653.0 0.205 = 150,2 kNm Współczynnik f}_x obliczono z tablicy 5.2 poz.b: ₆ Mi » 0,15 M? 71.0-0,15 • 13,3 ^P~ Mma, ~    71.0

6. Współczynniki długości wyboczeniowej

Założono projektowanie stopy sztywnej słupa w płaszczyźnie ramy, przegubowej — w kierunku podłużnym. Górny koniec słupa będzie nieprzesuwny (usztywniony tęznikami pionowymi dachu).

Współczynnik p*

Nie uwzględniono w obliczaniu sztywności zamocowania Ko wpływu sztywności tyfco pasa dolnego kratownicy, stąd przyjęto Ko***, ponadto:

n    ¹

^l'-°- *‘Ko^Kc*2

Z nomogramu 4.i8b przyjęto = 1,21.

Współczynnik p_y

Założono pełne usztywnienie tężnikiem pionowym górnej części słupa, stąd p>0; X2 = 0.95

Z nomogramu 4.188 przyjęto p_y=0,66.

Sztywność słupa

6io

ix 11,9

ase

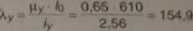
Współczynniki wyboczenia <p/

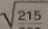
Xp = 84 ^-86.0

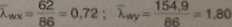
9tt — 0,887; <p«y * 0.295 7. Współczynnik zwichrzenia

Założono, że rygle ścienne zabezpieczać będą przed zwichrzeniem punktowo pas ściskany do momentu zginającego.

Stąd jako długość obliczeniową h = 0.3 + 2.4 - 2.7 m przyjęto odległość między stopą słupa a drugim kolejnym ryglem ściennym (rys.5.41):

Przyjęto «pł * 0.85 z tablicy 4.2 wg krzywej a.

Współczynnik poprawkowy A* :

a - 0.04 <0.1

Nośność słupa w płaszczyźnie zginania:

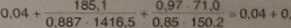
Nośność słupa w płaszczyźnie sztywności mniejszej

» 0.04 + 0.15 >0.6 -0.79 < 1

Ponieważ 0* = 1, nie sprawdzano słupa na nośność jednoczesnego zginania i ściskania (wzór 5.43).

8. Słup zawietrzny (prawy)

Ponieważ moment maksymalny w słupie prawym jest dużo mniejszy od momentu zginającego słupa lewego, a siła ściskająca jest nieznacznie większa, przyjęto także I 300.

6.7.5. Siły przekrojowe słupów stężających ram wielonawowych

dwukrotnie większe od reakąji słupów zewnętrznych. W obliczeniach sił wewnętrznych ramy wielonawowąj z rygiem podatnym wykorzystać można założenia i zasady stosowane do obliczania sił wewnętrznych najwyższej (pierwszą) z góry) kondygnacji ramy wielokondygnacyjną) (p. 6.8).

Dobór przybliżonej metody obliczeń sil wewnętrznych slupów zależy od sztywności rygla ramy. Siły wewnętrzne ramy wielonawowej z ryglami podatnymi (rys.6.27) oblicza się metodą ognisk, stosąjąc hipotezę portalową lub wspornikową w zależności od stosunku wysokości do rosptęco-ści ramy. Zakłada się, że obciążenie poziome P rozdziela się proporcjonalnie na nawy. stąd słupy środkowe będą przejmowały reakcje poziome

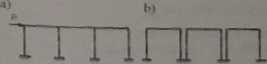
Ry».6.27

Wykorzyatiyąc założenie upraszczające zarówno metody portalową), jak też wspornikowej, obliczyć można siły wewnętrzne ramy wielonawowej. z ryglem bardzo sztywnym (kratownicowym).