37155 P3041027

6.7. Projektowanie słupów ram parterowych

ziomego obciążenia P_Q nie skróci się. czyli przemieszczenie górnych końców stupa będzie jednakowe, równe A. Na tej podstawie można przyjąć, że reakcje poziome będą sobie równe H\ = Ho=#*2- Pionowe reakcje i momenty zginające można obliczyć już z równań statyki.

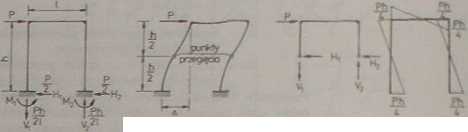
Ry».6.24. Schemat do obliczania ramy trzykrotnie Mn tycznie nicwyznnruilncj

Jednoprzęsłowa rama z węzłami sztywnymi f rys.6.24) jest trzykrotnie statycznie niewyznaczalna. Należy przyjąć 3 założenia upraszczające, aby w sposób przybliżony obliczyć siły przekrojowe od poziomego obciążenia.

Rys.6.25. Romo ze słupami nachylonymi

Jeśli założymy: (1) wartość jednej z poziomych reakcji. (2) położenie ogniska w punkcie przegięcia na lewym słupie. (3) położenie ogniska w punkcie przegięcia na prawym słupie, to z równań statyki odciętej myślowo ramy (rvs.6.24c) możemy obliczyć pozostałą poziomą reakcję i reakcje pionowe. Momenty utwierdzenia obliczymy z warunków równowagi odciętych myślowo wsporników. Na rvs.6.24a pokazano reakcje, a na iys.6.24d momenty utwierdzenia. Również w sposób przybliżony można wyznaczyć reakcje ram ze słupami nachylonymi (rys.6.25c, d). Obliczanie takich ram stężonych (rys.6.25a, b) wymaga zastosowania bardziej dokładnych metod. Jest jeszcze bardzo istotne, aby prawidłowo ocenić stopień utwierdzenia obu końców każdego słupa. Jeśli obydwa końce słupa są w pełni utwierdzone, to punkt przegięcia, czyli ognisko, przyjmuje się w środku wysokości słupa, a wtedy moment zginający przy głowicy i stopie będzie równy połowie wartości momentu zginającego słupa przegubowo umocowanego, przy tych samych warunkach geometrycznych i obciążenia. Przy różnych stopniach utwierdzenia punkt przegięcia przyjmuje się bliżej końca mniej usztywnionego.

Jeśli sztywność rygla ramy jest dużo większa od sztywności słupa (JrA, -* •*), to pomija się wpływ momentu zginającego słupa na moment podporowy rygla w kombinacji obciążeń pionowych i poziomych, a także wpływ podporowego momentu zginającego rygla na wartość momentu zginającego słupa.

Siły przekrojowe od obciążeń pionowych rygli pełnościennych oblicza się klasycznymi metodami mechaniki budowli, np. metodą przemieszczeń, Crown.

MMMM

ApnyMl

_Zapłt*_tWo^

Madzte 2.1.

Rozwiązanie

1 Oboąłento i «4y orrekrotowe od wwev Obciążenie skabOTt no śctonyl dach ae-

I itawtono na rys. 2.4 Zaftólmy. M ww> [rycina obciążenie wteimm dztafla fy*o na stront nawietrzną (rys $ Me) Ponadto pnyprjmy. Ja punkty pnagt-cia ;n,i|duia s*t w potowts wyaoaoeei [ słupa mitdzy stopami a pasami dolnymi i kratownic. Równiej paygrtjaiy. Ja obciążam# wiatrom dnamące nm odnąlą „ pr/egubemi górną część ramy. osdPśi się jednakowo na reakcje pomna Parcia sumaryczna wiatru na stront w

[ wietrzna z rys.24-

p - MO *• 375 - 1035 Pa

W 1035 J0*U1 ktoMi H'l - «'p= 13.8 KN

Reakcje poHoaw całej ramy

H • 13.8 * 6.21 3.05 32.75 kN

Reakcja pionowa:

yr, . _v .*** 4.48* 0.5

V-_ _ tao

W

*33«di

Bfla ścinająca na postom* pasa do mego kratowaicy Jad H bono. la reakcja poziome stopów w punktach przegitcw są M ścinających w stopre lewym obrazie rys«26b Momenty sgtna/ące — w stopach stopów

A#t - e.21 3.00* 0.5 * I3 d 3.06* 71.0 kNm H>- Ul 3.06 • 42.1 kto*

I— na pozKNTWe paea dolnego kratoantoy

Ml - 32.75 6.1 71.0 -6,21 ft9* 0 5 - 1X3 kMm - 42.1 - 13,8 6.1 * -42.1 kNm Wykresy momentów rgmatącycn Hf swego i

M6 26d.

2 Obciążenia pionowe i aśy oeiewa w stopie W komhewcjl z oOaąjenłem metrem m *ą> dbato* 3 atmąfmm śnieg, udźwigi ekaktrowoągow Przy**) ittoipnil l—MWW Mahu VI - 1. udźwigów ta*0A śiaspi vs- 06 Kombinacja obdąjaś obsczemowych: stałe z przykładu 2 t. poz2 I I

zero. gdy

li) 0.0 6.0

54.0 kN