P3200149

220 Aiialua skupień

pf zestrzeiii cech (A. . A .). IV dwa punkty, a ściślej mówiąc wektory O A i OB, rc prezentują dwa obiekty (zob. rysunek 4.2). Interesuje nas odległość między nimi Wyznaczymy ją w drodze następującego postępowania: Rysujemy okrąg o pro mieniu 1 o środku w punkcie (0,0) i rzutujemy punkty .4 i B na ten okrąg. Ich rzutami są punkty odpowiednio .4 oraz B - są nimi punkty przecięcia półprostych o kierunku danego wektora z okręgiem. Wyznaczamy odległość euklidesową między rzutami .4 i B Będziemy ią określali jako odległość cięciwy (ang. chorddisc tancc) między punktami .4 i R tzn J'* (AB) = d^ai(A B ). Odległość cięciwy można wyprowadzić z twierdzenia cosinusów. Oznaczmy w tym celu boki trójkąta0A B QA = a, OB = b oraz .4 B = c. a także kąt wektorów a. Zapiszmy więc, że [j ' (.4 B )]* = t■' = j ~+b * — 2a b cos a. Ponieważ z założenia a = b'= 1 (promień okręgu), to [d“’(.4 B )|‘ = 1* + 1^J — la b' cos a =2(1— cos a). Odległość cięciwy możemy zatem zapisać za pomocą wzoru

i„ |    cos(a)J    (4.28)

(zob. wzór 4.26, a także książkę Ludwiga i Reynoldsa, 1988).

*

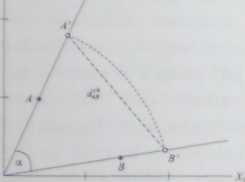
Rysunek 4.2. Ilustracja odległości cięciwy Źródło: Pielou. 1984

Nazwa tej miary wywodzi się stąd, że jest to długość cięciwy - odcinka łączącego dwa punkty okręgu, dla której odpowiadającym wypukłym kątem środkowym jest kąt a. Odległość cięciwy przyjmuje wartości z przedziału od 0 do v 2, podobnie jak względna odległość euklidesową (zob. wzór 4.11).

Odległość cięciwy jest to więc miara odległości oparta na cosinusie kierunkowym. Przypomnijmy, że w punkcie 1.6 zdefiniowano cosinus kąta między wektorami zmiennych x _i i x_k. Przez analogię możemy zdefiniować cosinus kąta między wektorami x_r i x_f, reprezentującymi obiekty. Nazywamy go kątowym rozdzieleniem (ang. angular separatioń) i zapisujemy

ii_#ł,

cm(a). = -j*"    (4.29)

Jłx! Zx\

1 m * m ^m

Zauważmy, ze co*(a) jest współczynnikiem korelacji międz\ ,.ccnirowan\ mi obiektami (zob wzór 4 24). a zatem cosinus kierunków \ podobnie }ak współczynnik korelacji q_lt. jest miarą podobieństwa obiektów typu korelacyjnego (ang. correlation-type measurc) Ponieważ przyjmuje on wartości od 1 do 1. me jest dość satysfakcjonujący jako miara podobieństwa i jest przekształcany w odległość cięciwy Warto jeszcze podkreślić, żt analogiczny wynik 4 28' otrzymamy jeśli wyznaczymy odległość euklidesową dla transformowanych wartości cech według

wzoru x„ = x_m / . X x _m.

Th ⁹

4.3.3. Wskaźniki podobieństwa obiektów według cech alternatywnych

Własności, ze względu na które porównujemy obiekty. mogą nnec charakter jakościowy, a te z kolei są często ujmowane alternatywnie tzn stwierdza się u obiektu obecność cechy lub jej nieobecność Macierz obserwacji X cech allema ty witych może być przedstawiona w ten sposob. ze zawiera tylko wartości 1 lubO. które oznaczają odpowiednio obecnosc i nieobecność cechy. a zatem

(430)

₌ j¹ 8dy cecha jest obecna 1° 8dy cecha nie jest obecna ^dla ‘ * ^{1 n oraz} > =    P

Dwa obiekty są identyczne, jeśli x _f = x _t (r.s — 1.....n . r* si tzn gdy wy

stępuje pełna zgodność współobecności i współ-nieobecności cech Podstawową więc zasadą, jaka przyświeca konstrukcji wskaźników (współczynników indeksów) podobieństwa, jest określenie liczby zgodnych wystąpień lub liczby wspólnych cech w stosunku do łącznej liczby cech Nie ma formalnych przeszkód, aby dla cech binarnych wyznaczać kw adratową odległość euklidesową

(4.31)

gdzie U„ - a-,.)²

0    gdyx„«x,-l lub x,=x,«0

1    gdy

która jest po prostu liczbą niezgodnych w ystąpień Może być więc ona użyta do mierzenia podobieństwa, choć ma tę negatywną cechę, że jednakowo traktuje zarówno współobecności (1 — 1), jak i współ-nieobecności (0 — 0). Uważa się jed-