P3200158

244 4. Analiza skupień

4.4. Podobieństwo cech i jego pomiar

244 4. Analiza skupień

Grupowanie zmiennych wymaga, podobnie jak w przypadku grupowania obiektów, pewnych numerycznych miar podobieństwa, które powinny charakteryzować zależności między zmiennymi. Rozważając pewną liczbę p zmiennych,

kwestią w analizie skupień dla cech jest porównywalność miar powiązania, tak aby wyższa wartość miary jednoznacznie wskazywała na silniejszą zależność niż wartość niższa. Uwaga ta ma związek z wcześniejszą dyskusją na temat zmiennych różnego typu i wieloma różnymi miarami podobieństwa (zależności, asocjacji) typowymi dla poszczególnych rodzajów zmiennych. Ważne jest przy tym, aby stosowane miary podobieństwa były symetryczne.

4.4.1. Pomiar podobieństwa cech ilościowych na podstawie korelacji Współczynnik korelacji Pearsona

r

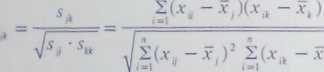
(4.52)

jest bardzo naturalnym miernikiem podobieństwa cech. W przeciwieństwie do oceny podobieństwa obiektów, gdzie wskazuje on raczej na podobieństwo profili obiektów, a nie na bezwzględne podobieństwo w rozumieniu zbieżności wartości cech (zob. punkt 4.3.2), tutaj - zgodnie z istotą pomiaru współzależności - idealne podobieństwo cech, to sytuacja w pełni identycznych lub proporcjonalnych wartości u obiektów (liniowa dodatnia zależność funkcyjna) pociągająca za sobą wartość 1 współczynnika korelacji. Zmienne o wysokich ujemnych korelacjach są traktowane jako bardzo niepodobne.

Współczynnik korelacji parami jest właściwy dla typowych zmiennych ilościowych, mierzonych w skali interwałowej lub ilorazowej. W przypadku zaś, gdy cecha jest mierzona w skali porządkowej, czyli obiektom przypisano kolejne liczby naturalne zgodnie z przyjętym kierunkiem nasilenia badanych własności (lub inaczej: obiekty zostały porangowane), to za miarę podobieństwa należy przyjąć współczynnik korelacji rang Spearmana

6 2 D²

i =1

(4.53)

w

. ₄ podobieństwo cech i jego pomiar______ 245

Współczynnik korelacji Spearmana jest współczynnikiem korelacji parami dla liczb naturalnych. Można więc do pomiarów w skali porządkowej zastosować tizór (4.52).

W miarę potrzeby można korzystać również z innych miar korelacji, jak na przykład ze współczynnika zgodności uporządkowań T-K.endalla

4.4.2. Pomiar podobieństwa cech nominalnych

Rozważmy teraz cechy jakościowe - nominalne Niech dwie cechy A i B mają określoną pewną liczbę kategorii (klas, odmian), odpowiednio r i s Ich rozkład u n badanych obiektów jest przedstawiany w postaci tablicy kontyngencyjnej (wielodzielczej) o wymiarach r X s, a więc o r wierszach i s kolumnach (zob tablica 4.2). Iloczyn r • s określa łączną liczbę klas klasyfikacyjny ch typu A B (lub komo rek tablicy odpowiadających A, i B₍) .

Tablica 4.2. Schemat tablicy kontyngencyjnej

	Cecha B			1
| Cecha A	B,	b2	-__Ł_
A,	"11	"12		_Hi:_1
A2	"21	"22	"2j	1__1
				_I_
A,	"rl	tlf2		1__1
1_h-	n.i	1 ^nrl.....-	n.j

Poszczególne oznaczenia w tablicy mają następujące znaczenie r - liczba klas cechy A (i = 1,2,... ,r), s - liczba klas cechy B (j= 1,2,..., s),

n -liczbaobiektów' należących do i-tej klasy cechy A i równocześnie do i-tej kia sy cechy B, czyli do klasy AB (liczebność komórki AB).

n .= 2 n.. — liczba obiektów należących do i-tej klasy cechy A (niezależnie od

klasyfikacji ze względu na cechę B),

n.₍ = 2 n„ — liczba obiektów należących do /-tej klasy cechy B (niezależnie od klasyfikacji ze względu na cechę A),

n= 2 2 n_# — łączna liczba badanych obiektów (np. liczebność próby).

* Różnica między tablicą kontyngencyjną a tablicą korelacyjną polega na tym, że tablica korelacyjni zawiera pogrupowany rozkład liczebności o przedziałach określonych za pomocą wartości ob-Ktwowalnej zmiennej losowej i dlatego posiadających naturalne uporządkowanie i jasno zdefiniowaną szerokość.