58485 P3310033 (2)

217

4.1 Podobieństwo obiektów i jego pomiar

podczas gdy inne staną się mniej znaczące. Odwrotna sytuacja może dawać laki sam efekt.

Wartości odległości obliczane według powyższych wzorów zależą od liczby p uwzględnionych w badaniu zmiennych i rosną wraz z tą liczbą. Aby uwolnić się od wpływu liczby zmiennych, często uśrednia się odległości poprzez dzielenie przez p. Otrzymujemy w ten sposób następujące mierniki:

• Przeciętną odległość miejską (ang. mean absolute disiance)

si

w -

(4.7)

nowskiego² Jest ona niezbyt chętnie stosowana przez biologów, którzy wymię

zwaną też różnicą przeciętną, średnią różnicą cech lub odległością Czeka-

niają jako jej wadę to, iż zawsze niedoszacowuje odległość euklidesową (zob. Sne-ath i Sokal, 1973). Stwierdzenie to nie jest w pełni zrozumiałe. Przeciętna miejska odległość nie musi być analizowana pod kątem tego, jak szacuje ona przeciętną odległość euklidesową. Jest to jedna z możliwych metrycznych miar, wyjściowo ani lepsza, ani gorsza od innych. Relatywizowanie oceny przydatności średniej metryki miejskiej opiera się zapewne na analogii między odchyleniem przeciętnym a odchyleniem standardowym, przy uznawanej przewadze tej drugiej wielkości jako miary rozproszenia. Jakkolwiek byśmy oceniali obie miary odległości to dla wielu danych oba pomiary okazują się jednakowo dobre z punktu widzenia wyników grupowania.

• Przeciętną odległość euklidesową (ang. mean euclidian distance)

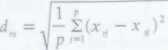
(48)

Ciekawy wynik w odniesieniu do przeciętnej odległości euklidesowej uzyskał F.J. Rohlf (zob. Sneath i Sokal, 1973). Stwierdził on mianowicie, iż przy p standaryzowanych niezależnych zmiennych o rozkładzie normalnym, wartość oczekiwana wielkości d dla parzystej liczby p(p£ 4) wynosi

21 Średnią odległość miejską w badaniach antropologicznych użył 1 .C zekanowski już w 1909 roku i nazwał ją: durchsehniil liche Differenz Faktu tego zdają się często nic dostrzegać liczni angielskojęzyczni statystycy, choć wzmiankę o wykorzystaniu metryki miejskiej przez Czckanowskicgo zamieścili w swych książkach: Sneath i Sokal (1973) oraz Everitt (1993).