P3200161

250

.lAnali^k^..

ujemnym .

• Współczynnik powiązania Yulea (ang. coęfficient of colligation)

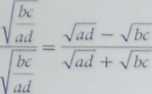
1 +

(470)

który ze współczynnikiem Q_lk pozostaje w następującej relacji

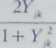
(471)

Współczynniki asocjacji i koligacji są niezależne od liczebności brzegowych: (a + b\ (c + d), (a + c) oraz (b + d), czyli inaczej - są niezależne od względnych proporcji (a + b) i (c + d) występujących w danych. Ta własność jest ważna z tego względu, że współczynniki Q_lk i Y^ można stosować w sytuacjach, w których proporcje są dowolne⁶¹.

• Współczynnik Edwardsa (ang. cross ratio)

(4.72)

_bc_ ^ik ~ ad

który jest prostym wykorzystaniem kryterium niezależności. W tej postaci oraz w postaci logarytmicznej był on wykorzystywany w badaniach genetycznych (zob. Anderberg, 1973)⁶². Przy założeniu, że ad 0, pozostaje on w określonych relacjach z dwoma poprzednimi współczynnikami

Y

(4.73)

• Współczynnik korelacji tp Yulea-Boasa

ad — bc

^>k -J(a + b)(c + d)(a + ć){b + d)

(4.74)

⁶⁰ O całkowitym skojarzeniu dodatnim mówimy, jeżeli wszystkie A są B lub wszystkiej! są_Ą

zależnie od tego, czy mniej jest elementów A czy też B. Wówczas w tablicy 2x2 komórka AB lub AB jest pusta, czyli b = 0 lub c = 0. Podobnie całkowite skojarzenie ujemne wystąpi w przypadku, gdy żadne A nie jest Z? lub żadne nic-A nie jest nie-A czyli a = 0 lub d = 0 (zob. Yule i Kcndall. 1966).

⁶¹    Są to na ogół sytuacje doświadczalne: np. grupa kontrolna i grupa badana.

⁶²    Analogicznie konstruowana miara występuje w badaniach medycznych (np. epidemiologicznych) pod nazwą ryzyka względnego lub ilorazu szansy (ang. odds ratio) i jest ilorazem iloczynów zgodnych i niezgodnych wystąpień cech (np. chory - zdrowy; narażony - nienarażony): (a / b):{c / d) = ad / bc.

fO cech i jego pomiar

251

mniejsza z tych dwóch sum,

(j i (}' - dopełnienia sum odpowiednio większej i mniejszej do liczby n (czyli pozostałe sumy brzegowe).

Najwyższą wartość współczynnik <p przyjmuje, gdy tablica jest symetryczna czyli gdy (n + c) = (b + d) i (a + b) = (c + d). Dla każdej innej kombinacji liczebności brzegowych jest ona niższa, przy czym obniża się w miarę zwiększania lub zmniejszania liczebności (a -f.:) lub (a + b).

Można wykazać, że współczynnik ip . jest współczynnikiem korelacji Pear-sona (według momentu iloczynowego) r_jk (wzór 4.52) dla systemu danych 1 -0 gdzie poszczególne elementy w zoru na współczynnik korelacji parami są identy filcowane następująco (zob. Anderberg, 1973)

=a + b, 1!y₍.=fl + c, 2    =<j, 2.v;^L =a + b, 2y;=s+c (4.76)

Przez analogię do miary kątowej, tzw. rozdzielenia kątowego opisanej Hpunkcie 4.3.2 (wzór 4.29), można zdefiniować miarę korelacyjną - cosinus kąta między wektorami zmiennych ; i k

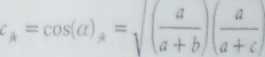
(4.77)

i jest niczym innym jak indeksem Ochiai dla cech (por punkt 4.3.3). który jest średnią geometryczną z dwóch ilorazów a / (a + b) oraz a / [a + c).

® A więc inaczej niż w przypadku poprzednich współczynników