P3200162

252 4 Analizą skupią,

Współczynnik skojarzenia oraz współczynnik korelacji (p _jk można również obliczać, jeżeli w tablicy asocjacji zamiast liczebności bezwzględnych mamy udziały (częstości względem n). Wówczas symbole a, b, c, d tak właśnie należy rozumieć. Współczynniki <p _lk oraz powinno się w zasadzie używać wtedy, gdy są nieujemne, gdyż wówczas są najbardziej efektywne (zob. Timm, 2003).

Zestawienie obliczonych p{p — 1) / 2 miar asocjacji podaje się w formie macierzy podobieństwa

s,

1 ... s

1 S

(4.78)

z tym że dobrze jest dla ułatwienia interpretacji cechy z wysokim dodatnimi wartościami indeksów umieszczać wzdłuż przekątnej macierzy. W macierzy można by też podawać wartości dwóch wskaźników - jeśli są obliczane - jednego nad przekątną, drugiego zaś pod przekątną.

Wychodząc ze współczynników <p _jk oraz c ^, można obliczać odpowiadające im miary odległości, które można wykorzystać w grupowaniu cech. Są to:

^dl    =J^l~<P’^dl =1“^ lub ^d)_k = ■_N/ł ~ ^cik •

Zaprezentowane w tym punkcie postępowanie jest dość uciążliwe, albowiem mierniki podobieństwa cech alternatywnych są wyznaczane dla każdej pary cech odrębnie - tworzy się odrębne tablice asocjacji, z których oblicza się wartości mierników. Istnieje jednak znacznie szybszy sposób, który krótko omówimy⁶⁴. Jak wiemy z punktu 4.3.3 macierz obserwacji X dla danych alternatywnych może być przedstawiona jako zbiór 1 lub 0, w zależności od obecności lub nieobecności każdej z cech X_j(j— 1,... ,p) w obiekcie. Oznaczmy przez

(4.79)

liczbę obecności każdej z cech w zbiorze n obserwacji, lub inaczej liczbę obiektów, które posiadają cechę X_i (/ = 1,..., p), oraz przez

(4.80)

= 2 X_ijX_lk    fgj11I-... * pi i * *)

⁶⁴ Fragment ten zamieszczamy, pomimo że w rozdziale 4 główny nacisk kładziemy na klasyfikację obiektów w wielowymiarowej przestrzeni cech. Problem bowiem można odwrócić i grupować cechy w wielowymiarowej przestrzeni obiektów, co w wielu zagadnieniach ma konkretny praktyczny wymiar.

icństwo cech i jęgopomiar

253

₀ółwystąpień lub połączeń (koincydencji) cech X \X_t w zbiorze jed-

W*r '

r |_Ujj inaczej liczbę jednostek, które posiadają zarówno cechę X , jak i cechę y n_# i tworzą symetryczną macierz N = (n,} obecności (liczby na •V j współobecności (pozostałe elementy)

«.«	^WI2 •	n,
^n2l	^n22 *	n. 2f
>	*,2 •	n PF

N =

(4.81.

p^y _ty_Ch warunkach miarą podobieństwa cech jest współczynnik korelacji

fll

P*⁸⁵

ⁿ' ⁿ/t ~ ⁿ, ' ⁿkk

* ■Jn_i'n_kt(n’-n_iXn-nJ

(4.82;

Jest to klasyczny współczynnik korelacji dla cech binarnych a zatem przy •_e wartości z przedziału [-1, 1]. Warto zasygnalizować również, ze macierz wystąpień i współwystąpień N jest iloczynem macierzy wyjściowej X i jej trans pozycji. N = X^TX(zob. Dagnelie, 1975).

pnykład 4.2. (współczynnik korelacji punktowej)

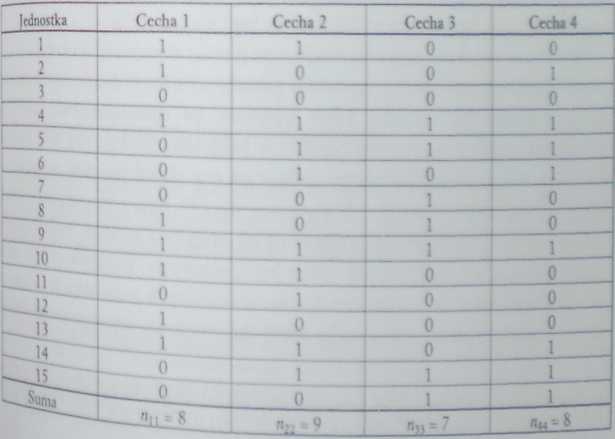
Załóżmy, że zbadano n = 15 jednostek ze względu na p = 4 cechy alternatywne, zapisując wartość 1, jeśli cecha (wyróżniona odmiana cechy ) występuje, oraz wartość 0 w przeciwnym przypadku. Macierz danych binarnych podajemy w postaci następującej tablicy: