15728 P3200144

216

⁴-Analiza skupią

kioi 4 możemy zapisać również w postaci

«²')² =(x - X J(x, - xj=||x, - X , II²    (4.6a)

gdzie x’, oraz x’, wektory wierszowe (IX p),

J| x. — x . )| - euklidesowa norma wektora (x, — x _f)

Takie podejście do mierzenia odległości jest zalecane, jeśli w grupowaniu hie-rarchic/n>m stosow ane są metody: centroidalna, Warda, średniego zróżnicowania lub surm kwadratów (zob. punki 4.6). Kwadratowa odległość euklidesowa jest zawsze wyborem bezpiecznym. Podobnie jak w przypadku metryki miejskiej metrykę euklidesowo można stosować, gdy zmienne są wzajemnie nieskorelo-wane. co jest warunkiem trudnym do spełnienia. W przeciwnym przypadku metryka euklidesowa będzie złą miarą odległości (Everitt, 1993) i wówczas zalecaną miarą odległości jest odległość Mahalanobisa²⁰. Nie wydaje się, aby to ograniczenie było w praktyce uwzględniane.

Jakkolwiek metryka euklidesowa jest najpowszechniej stosowaną miarą zróżnicowania, to wielu badaczy woli stosować metrykę miejską. Argumentują oni, że metryka miejska spełnia następujący warunek: jeżeli dwa obiekty są opisane dwiema zmiennymi, których jednostki skali są jednakowe, to mają one tę samą odległość bez względu na to, czy są oddalone o dwie jednostki ze względu na każdą zmienną, czy też o jedną jednostkę ze względu na jedną zmienną i o trzy jednostki ze względu na drugą zmienną, co czyni z niej naturalną miarą odległości (zob. Everitt, 1993). Poważny natomiast zarzut formułuje się pod adresem metryki eu-kiidesowej, taki mianowicie, że w przypadku zmiany skali pomiarowej nie zachowuje ona nawet porządku odległości. Everitt (1993) daje przykład trójki dzieci, którym zmierzono wagę (w funtach) oraz wzrost (w stopach). Dla danych 1(60:3,0), 11(65:3,5) oraz 111(63:4,0) mamy następujące odległości euklidesowe: d_u = 5.02 d_n = 3,16 oraz d_2i = 2,06. Jeśli natomiast wzrost zmierzymy w calach, to odległości euklidesowe wyniosą: d_}, = 7,81, d_l} = 12,37 orazd₂, = 6,32idziecko I będzie teraz traktowane jako bardziej podobne do dziecka II niż do III. Zanim więc obliczy się odległości euklidesowe dobrze jest przeprowadzić standaryzację zmiennych według wzoru x_if/s. . Jest to zarzut prawdziwy, ale odnosi się również do odległości miejskiej, która także zmienia porządek odległości przy zmianie skali pomiarowej zmiennej lub zmiennych (zob. Hair i in., 1995). Właśnie zmiana skali (pomiar nie w stopach, lecz w calach; nie w minutach, lecz w sekundach itp.) powoduje, że zmienna prześladowana zacznie dominować w obliczeniach, ¹

podczas gdy inne staną się mniej znaczące. Odwrotna sytuacja może da w a' taki sam efekt.

Wartości odległości obliczane według powyższych wzorów zalezą od liczby p uwzględnionych w badaniu zmiennych i rosną wraz z tą liczbą Aby uwolnić się od wpływu liczby zmiennych, często uśrednia się odległości poprzez dzielenie przez p. Otrzymujemy w len sposób następujące mierniki • Przeciętną odległość miejską (ang tntan absuluu disianui

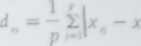
<47

zwaną też różnicą przeciętną, średnią różnicą cech lub odległością Czeka -

niają jako jej wadę to, iż zawsze niedoszacowujc odległość euklidesow ą ■ zob Sne ath i Sokal, 1973). Stwierdzenie to nie jest w pełni zrozumiałe Przeciętna miejska odległość nie musi być analizowana pod kątem lego jak szacuje ona przeciętną odległość euklidesową. Jest to jedna z możliwych metrycznych miar wyjściowo ani lepsza, ani gorsza od innych. Relatywizowanie ocen\ przydatność: średnie’ metryki miejskiej opiera się zapewne na analogii między odchyleniem przecięt nym a odchyleniem standardowym, przy uznawanej przewadze tej drugiej wiei kości jako miary rozproszenia. Jakkolwiek byśmy oceniali obie mian odległości to dla wielu danych oba pomiary okazują się jednakowo dobre z punktu widzenia wyników grupowania.

• Przeciętną odległość euklidesową ( ang. mcan cuciidian disiance

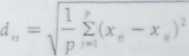
48

Ciekawy wynik w odniesieniu do przeciętnej odległości euklideso¹ ei uzyskał F.J. Rohlf (zob. Sneath i Sokal. 1973). Stwierdził on mianow icie iż przy pstanda ryzowanych niezależnych zmiennych o rozkładzie normalnym, wartość oczekiwana wielkości d dla parzystej liczby p(p > 4) wwnosi

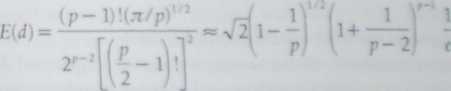
(.4.9)

²¹ Średnią odległość miejską w badaniach antropologicznych użył 1 ('zekanowski już w 1909 roku

i nazwał ją: durchschnittlicht Diffcrcnz Faktu tego zdają się często nic dostrzegać liczni angielskojęzyczni statystycy, choć wzmiankę o wykorzystaniu metryki miejskiej przez Czekanowskiego zamieścili w swych książkach. Sneath i Sokal (1973) oraz Everitt (1993)

1

Odległość Mahalanobisa dla dwóch obiektówr i s dana jest wzorem d_n = (x_r — x₍ )S^_,(x_r -x,l gdzie x. i i, są wierszowymi wektorami pomiarów, zaś S macierzą kowariancji. Formuła odległości Mahalanobisa ma wbudowaną procedurę standaryzacyjną danych.