skrypt wzory i prawa z objasnieniami20

36

Praca

■ Dla stałej siły pracę wydłuż odcinka o długości / możemy zapisać również za pomocą iloczynu skalarnego dwóch wektorów

F / .

gdzie / jest wektorem przesunięcia (ma kierunek i zwrot przesunięcia ciała) Dla siły zmiennej definiujemy pracę elementarną d#'. czyli pracę dla tak małego przesunięcia d r . że dla mego siłę można uważać za stałą i wtedy prawdziwą jest poniższa relacja:

dU'=7d~r

Następnie sumujemy prace elementarne wykonane wzdłuż całej zadanej drogi otrzymując całkę z punktu 13

■    Przypomnijmy, że praca me musi być wielkością dodatnią Dla stałej siły. gdy kat u między przesunięciem a kierunkiem działania siły wynosi 90 . to praca zeruje się, natomiast, gdy a > 91) . to praca ma wartość ujemną.

■    Przykładem siły , której praca będzie zawsze mieć wartość ujemna jest siła tarcia (lub siła oporu ośrodka). Siły te z definicji mają kierunek przeciwny niż przesunięcie ciała Stała siła tarcia F_r wykona na drodze s pracę

W=-F_ts.

■ Niech innym przykładem wyznaczenia pracy, będzie praca wykonana przy bardzo wolnym podnoszeniu ciała na wysokość H Siła podnosząca ciało F

będzie wtenczas w każdym momencie ^ zrównoważona siłą ciężkości P - mg

Siły F i P będą na drodze H siłami stałymi Kąt    między siłą F    a

H

przesunięciem jest równy zeru. a więc ostatecznie praca siły F wyniesie W_F = FH eosO" = FH= mglł Kąt między silą P a przesunięciem jest równy 180'. a więc praca siły P wyniesie W_P = PU cos 180' = - PU = -mgłł Dla człowieka podnoszącego ciało najważniejsza    jest    pierwsza    z

ir

wyznaczonych prac. gdyż jest to praca, którą on będzie musiał wykonać Dla mego nie będzie miało znaczenia to. ze w tym przypadku siła wypadkowa wynosi zero i oczywiście praca siły wypadkowej W- W p + IVp    0

13. Praca

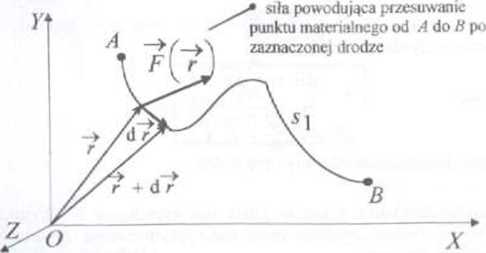
praca siły pr/csuwająccj punkt materialny od A do B po drodze s_t

^WA~>B =. s	[ ^ l	/ ^51	Fxdx + Fydy + F:dz\
całka po drodze <	^ iloczyn skalamy wektora siły

s, od A do fi    F = [F_x{x,y,z), />(*.>', 2), F_:(x,y,z)]

i wektora elementarnego przesunięcia d^ = fdx,d>,(bl

13.1 Praca stałej siły

stała co do kierunku działania i wartości iila działająca na ciało

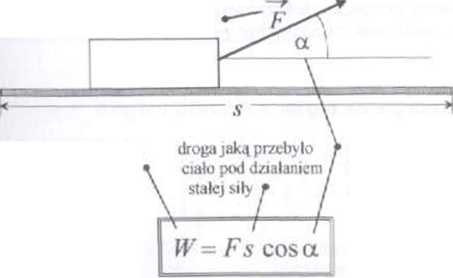
stały kąt między kierunkiem działań':* sih a kierunkiem przesunięcia

praca wykonana przez siłę ciągnącą ciało