P3200178

•S4 4 Analiza skui Pień

Jrugiauuc. które traktuje się jako poziomy, na klor> eh jednostki pojawiają się p₀ raz ptcrwsz> w skupieniu. Odwołując się do przykładu 4.3 (zob. punkt 4.6.2) można na podstawie zamieszczonego tam dendrogramu zapisać macierz po nomow łączenia C — U\ 1, zwaną macierzą dendrogramu lub leż macierzą kofenc tyczną ¹

•S4 4 Analiza skui Pień

n(n-l)

i

f \	2 ‘
Ed"
/<* >

n(n -1)    ₂

Z c.

(4.110)

0	2,75	3,50	4,17	3,18	3,18	2.75
2,75	0	\50	4,17	3,18	3,18	2,17
3,50	3,50	0	4,17	3,50	3,50	3,50
4,17	4.17	4.17	0	4.17	4,17	4.17
3,18	3.18	3.50	4.17	0	2.51	3,18
3,18	3,18	3.50	4.17	2,51	0	3,18
2.75	2,17	3.50	4,17	3,18	3,18	0

Znaczy to, że elementami macierzy kofenetyeznej są poziomy łączenia, na których para obiektów łączy się w tym samym skupieniu pierwszy raz. Spełniają one nierówność ultramettyczną c_H < max(c_iu.,c_iH.). Jednym z możliwych sposobów oceny dopasowania jest obliczenie współczynnika korelacji według momentu iloczynowego między odpowiadającymi sobie odległościami w obu macierzach D i C_AmJr, który odpowiednio do nazwy macierzy nosi nazwę współczynnika korelacji kofenetyeznej (ang. cophenetic correlation coefficient).

gdzie sumowanie rozciąga się na wszystkie n(n — 1) / 2 par obiektów. Współczynnik można zapisać także w postaci

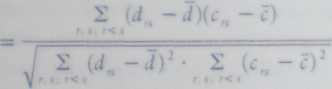
(4.111)

gdzie d =- £ d . podobnie jak ć.

2    r.s;r<*

Wysokie wartości współczynnika wskazują, że dendrogram daje dobre pod-sumowanie obserwowanych różnic między obiektami lub podobieństw obiektów. Współczynnik korelacji kofenetyeznej był badany przy założeniu, że grupowane obiekty stanowią próbę losową pochodzącą z populacji o wielowymiarowym

_|it/.kład/ic ih»i mulityni Stwicrdzuuu, 1/ v>aitosc wspołc/.yunika przct tętnic iiu [1 je w t u/. zc w/jo&lcm liczby obiektu w n 1 piawic nu zuiczy od liczby zmiennych ^l^iculzono ponadto, ze wartość współczynnika powyżej 0,8 jest zwykle wy starczająca do odrzucenia hipotezy o biaku zgodności elementu w macierzy D 1 i, \Vyiiiki dalszych badan przestrzegają jednak ze nawet wartość współczynnik* około 0,9 nie musi gwaianlowae lęgu ze dcndi ugrani jest dostatecznie dobrym podsumowaniem relac ji fenetycznych Oznacza Lu, ze współczynnik koielacji ku lenctyeznej musi być wysoki, aby można było bezpiecznie zakładać zc dane mają hierarchiczną strukturę grupową** przykład 4.10. (korelacja kofenetyczna)

Zbadamy zgodność odległości w' macierzy O z przykładu 4 '< 1 odległości dendrogramów z przykładów 4.3-4.9 Odległości zaobserwowane , udkgłusc 1 u<. ndrogramów oraz obliczone współczynniki korelacji kolcnetycznc • podam-w tablicy 4.6.

Tablica 4.6. Odległośc i d_n w w yjściowej macierzy odlcgłos- O . odległość. dcndrogiamo

	Macierz	Metoda	Metoda		Metoda			Mr torii
Pary		najbliższego	najdalszego		średniej		HicUi^Jł v			Waads
obiektów		sąsiada	sąsiada		grupowej
r 1-2	4.23		9.21		3.490 i	3,39So	3.3986	*.42735		,2642 1
1.1	3.50	3.50	3.50		5.650 1	6.1283	5.1874 j	‘.5<Zajc		5.5Wb_
1 -4	7.64	4.17	9.23		6.225 _j	5.2381	5.7274 |	890123
" 1-5	5.11	3.18	9.23		6.225	5.2381	5.7274 T	8.30123		V2>5?“
F 1-6	4,05	3.18	9.23		6.225 |	5.2381	5.72'4 j	8.90123
	2.75	2.75	9.23		3.490 i	5.398o	3.3986 J	6,42 55		' JM?
" 2- 3	8.54	3.50	9.23		5.650 I	6.1283	5.1874 |	6.42735		*2*42
2-4	5.19	4.17	8.37		6.225	5.2381	5,7274 1	8.90123
^ 2-5	6.78	3.18	8.37		6.225	5.2381	5,7274 1	S9U12'
2-6	3.18	3.18	8.37		6.225 .	5.2381__	5,7274 I	8.90123
2-7	2.17	2.17	2.17			2.1700	2.1 ~00 1	2.1 7000		2.1 ^7OO ^1
5-4	6.20	4.17	9.23		6.225	6.1283	5.7274 ]	890123		9.85?'
3-5	7.58	3.50	9.23		6.225	6.1283	3^7274 |	8.90123		tJtM7 j
5 6	9.23	3,50	9.23		6.225	6.1283	5.7274 j	8901?'		9.8S2“
L ^5 7	4.91	3.50	9.23		5.650 i	6.1283	5.iS74 ]	6.4?" 35		"2642
4-5	4.17	4.17	4.22		4.195	4.0029	4,0029 1	4.61625		4.6226
4-6	4.22	4.17	4.22	4.195		4,0029	4,0029	4.61625		4.6226
4- 7	5.72		8.37			5.2381	5.~."4	890123		9.852?
5 6	2.51	2.51	2.51		2.510	2.5100	2.5100 7	2.51000		Łyioo j
5-7	8.37	3.18	8.37		6.225	5.2381	s.~2~4 )	8.90123		9.852?
6- 7	5.65		8.37		6.225	5.2381	5.“2*4 ]	890123		9,852"
	X	0.4109	0.5789		0.6558 J	0.6^T46	0.655“	0.6184		0.61 ? I
	*	39.92	-47.44		0 1	8.30	7.93	- 38.24		-53.01
STRESS 1		0.4681				0.2741		0.4633

1

d.-c-ZdT c.

^w Wskazane własności współczyunika korelacji kofrnctyc/nei pochodzą z badań h L Kohlła iD.L. Fishera z lat 1969-70 i zostały zaczerpnięte z książki Kvcritta 1 Dunna (1991) Można przy okazji zapytać: Jeśli dane nic mają hierarchicznej struktury grupowej (co zresztą dendrograni powinien ujawnić), to czy wsp<jłczynnik korelacji kofenetyeznej może byc wysoki?