P3200182

292

4 Analiza .skupi,.,,

Liczba możliwych podziałów n obiektów na K grup jest duża. Fortier i Solo mon podali wzór rekurencyjny na liczbę N(n, K) różnych niebanalnych po-działów

N(n,K)=~ Kⁿ -

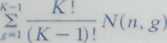
(4.122)

gdzie N(n.g) jest liczbą podziałów n obiektów na g grup (g = 1,..., K — 1).

W miarę wzrostu n i K liczba ta wzrasta bardzo szybko. Na przykład dla n — 19 oraz K = 8 wynosi ona /V(19, 8)> 1,7* 10¹² (zob. Gordon, 1981)¹⁰⁴ . Uwaga ta będzie ważna, jeśli przyjrzymy się istocie grupowania podziałowego.

Celem grupowania podziałowego jest znalezienie takiego podziału, w którym obiekty są podobne do innych obiektów należących do tej samej klasy, a niepodobne do obiektów należących do innych klas, albo - mówiąc innymi słowami -znalezienie takich podzbiorów obiektów, które są zarówno homogeniczne, jak i dobrze oddzielone. W tego rodzaju grupowaniu dla każdej określonej liczby K grup szuka się podziału, który jest optymalny ze względu na jakieś kryterium grupowania, nazywane przez niektórych badaczy miarą adekwatności podziału (zob. Hansen i Jaumard, 1997).

Metody grupowania podziałowego stanowią zbiór procedur niehierar-chicznych. które charakteryzują się tym, że tworzą niejako ostateczne skupienia, które nie zawierają innych skupień. Istnieje wiele odmian tej metody. Wśród nich dominują iteracyjne metody transferu zwane też technikami przemieszczeń (ang. iterative relocation algorithm, fr. method de transfert). Proces niehierarchicznego grupowania podziałowego techniką przemieszczeń można w skrócie wyjaśnić za Gordonem (1999) w sposób następujący: przy danym kryterium adekwatności podziału zbioru n obiektów na K rozłącznych klas należy zastosować odpowiedni iteracyjny algorytm relokacyjny, który wyszukuje optymalny, w sensie danego kryterium, podział obiektów. W tym postępowaniu można wyróżnić, w największym uproszczeniu, dwa etapy: 1) wstępny podział obiektów na K klas oraz 2) przekształcenia prowadzące do zmiany podziału w inny, lepszy podział obiektów Podział jest tak długo modyfikowany, aż żadna już transformacja nie poprawia przyjętego kryterium adekwatności podziału.

Liczba propozycji podziałowego grupowania jest duża, a różnice między nimi polegają na odmiennym podejściu do poszczególnych elementów postępowania, począwszy od definiowania kryterium optymalizacji podziału, poprzez wstępny podział obiektów, a kończąc na sposobach modyfikowania podziału (tj. sposobach przesuwania jednostek).

⁵⁰⁴ Por. liczbę Stirlinga drugiego rodzaju w punkcie 4.2.

Najstarszą metodą transferu jest metoda R I . Thomdik< a (1953)"' Fodsta v^owy algorytm metody był rozwijany przez lata Kolejne prace były często pro sadzone niezależnie, a ich efektem były nowe odmiany metody transferu Wymienić można następujących badaczy mających osiągnięcia na tym polu W.E. Forgy (1965), G.H Bali oraz D.j. Hall (1965; algorytm ISODATA), H.p. Friedman oraz j Rubin (1967). J MacQucen (1967; metoda K -means) F.M-L. Beale (1969), I£. Didey (1972; grupowanie dynamiczne), D.J McRae (1971), C.F. Banfield i L.C. Bassill (1977), J A Hartigan (1977). D Wishart (1978), a także A D. Gordon, P Hansen, B. Jaumard, 1. Hubert P Arabie i inni"" O ile grupowanie hierarchiczne można wykorzystywać do grupowania zmień nych, jako pomocnic ze narzędzie dla potrzeb redukcji przestrzeni cech o tyle gra powanie podziałowe¹ nie jest odpowiednie do tego celu Bo cóż miałby oznaczać i czemu służyć „optymalny” podział zbioru zmiennych charakteryzujących obiekty.

4.7.2. Kryteria adekwatności podziału

Kryterium adekwatności podziału w grupow aniu podziałowym jest istotnym jego elementem. Wyznacza ono zarówno przebieg postępowania modyfikującego po dział, jak i jego zakończenie W celu zddiniow ama kryteriów opracow ano pewną liczbę miar, które są dzielone na (zob Hansen i Jaumard 1997. Gordon 1999);

•    miary hetcrogeniczności (lub braku spójności) grup obiektów, oraz.

•    miary izolacji (lub oddzielenia) grupy od reszty danych

Miary te są oparte bądź to na własnościach mierzalnych cech obiektów i.r ), bądź też na odległościach między parami obiektów d_ś )

Aby omówić te miary, należy uściślić oznaczenia, którymi będziemy się posługiwali. Są one zgodne z oznaczeniami z innych rozdziałów na tyk. na ile jest to możliwe.

Niech x. (i = 1.....a: /= 1.....p) będzie wartośeią /-tej cechy u Mego

obiektu (czyli /-tą współrzędną i-tego punktu w przestrzeni p wymiarowej). Chcemy podzielić n obiektów' na K grup: C., C,.....C_k Oznaczmy przez n

liczebność £-tej grupy (g — 1.....A), przy czym 1 n = n. Wartość cechy /

obiektu i w grupie g będziemy oznaczali przez .y₍. . dodając do wcześniej podanego symbolu x_r trzeci subskrypt określający grupę, do której należy obiekt Dla każdej grupy możemy wyznaczyć centroid, czyli jej punkt ciężkości Współrzęd nymi centroidu grupy g są średnie wartości cech

105    R.L.THomdike. Whobdongsin thcfamil/'. Psychometrika, \ol 18.1955 (zob Dagnellic, 1975)

106    /,ob. Anderberg (1975). Dagnellic (1975). Lcbart i >n (1984). Gordon (1999)