13852 skanuj0012

408

Rys. 14.13

Rozwiązanie

Impedancja wejściowa wyrażona przy użyciu współczynnika odbicia ma postać

z - ^U' - z ^l+Me~^im - z ¹⁺    - z    \M\

^m    J, ” ^c 1 - Me-M¹ P 1 - \M\e-iW-W " ^c _emi~m _ |^| ’

stąd

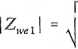
(lAfj • <Xisa)² + sin²a (cosor- |M|)² + sin²ar

|M|² + 2[A/|cosg + 1 ^ |M|²-2|M|cosa + 1

gdzie M = ~—4 \M\e^_t a = 2jS/ - ijr.

Moduł impedancji |Z_ml\ przyjmuje wartość maksymalną, gdy cosa = 1, czyli dla 2/3/ - i|r = 2krr,

stąd

,i. ifajL = M iśĘL. ;iiw«jfc4sŁ./

2/3    2/3    2 4ir

|Af|^2 + 2|M| +1 _	\M\ +1
\| |M[^2-2|M| + 1	\M\-1

Maksymalna wartość modułu |Z_UJ

Moduł impedancji |Z_W4l| przyjmuje wartość minimalną, gdy cosa - -1, czyli dla 2j3ł-

stąd

/ _ (2k+ 1)A ^ jrA. k - 0,1,2.....

4 4tt

Minimalna wartość modułu

Zakres zmian modułu impedancji wejściowej

Dla rozpatrywanego przykładu

\M\ + 1 |M| - 1		4|M|
|M| -1 \M\ + 1		|Af|^2- 1

Z₂ -Z_e

z^

* y ² , |M| =    , więc

AIZ^I = ^.

Przykład 14.13

Bezstratną linię długą o długości l = —, podaną na rys. 14.14, obciążono impe-

8

dancją Z₂. Należy obliczyć impedancję wejściową dla trzech wartości impedancji Z₂: a; Z₂ = R₂ +jX₂, b) Z₂ = c) Z₂ = jX₂. Dane: 7 = A, |H

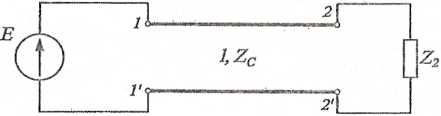
Rys. 14.14

Rozwiązanie

Impedancja wejściowa

= Z_cctg(ll

Z₂+jZ_ctgfil

Z_cctg/37₊/Z₂

_ _z ^z2 ⁺j^zc ^cz_c+jz₂

a) Dla Z₂=R₂+ jX₂

^wel *'^c 7 - Y + i R    ^Zj° r—~-^e

^ ^A2⁺/-«2    ₁/jR₂²+(Z_c-X₂)²

. ,    \3T₂ ⁺    IŁ.

gdzie: Z_c = |Z_C|, <p_Ł = arctg——, <p₂ = arctg--- ■■. ₄

^K2    A: X₂

1M|^2-2|M| + 1 _	1M|-1
\ |M|^2 + 2|M| + 1	\M\ +1

1

^Z«wlLn ⁼