17196 img323 (3)

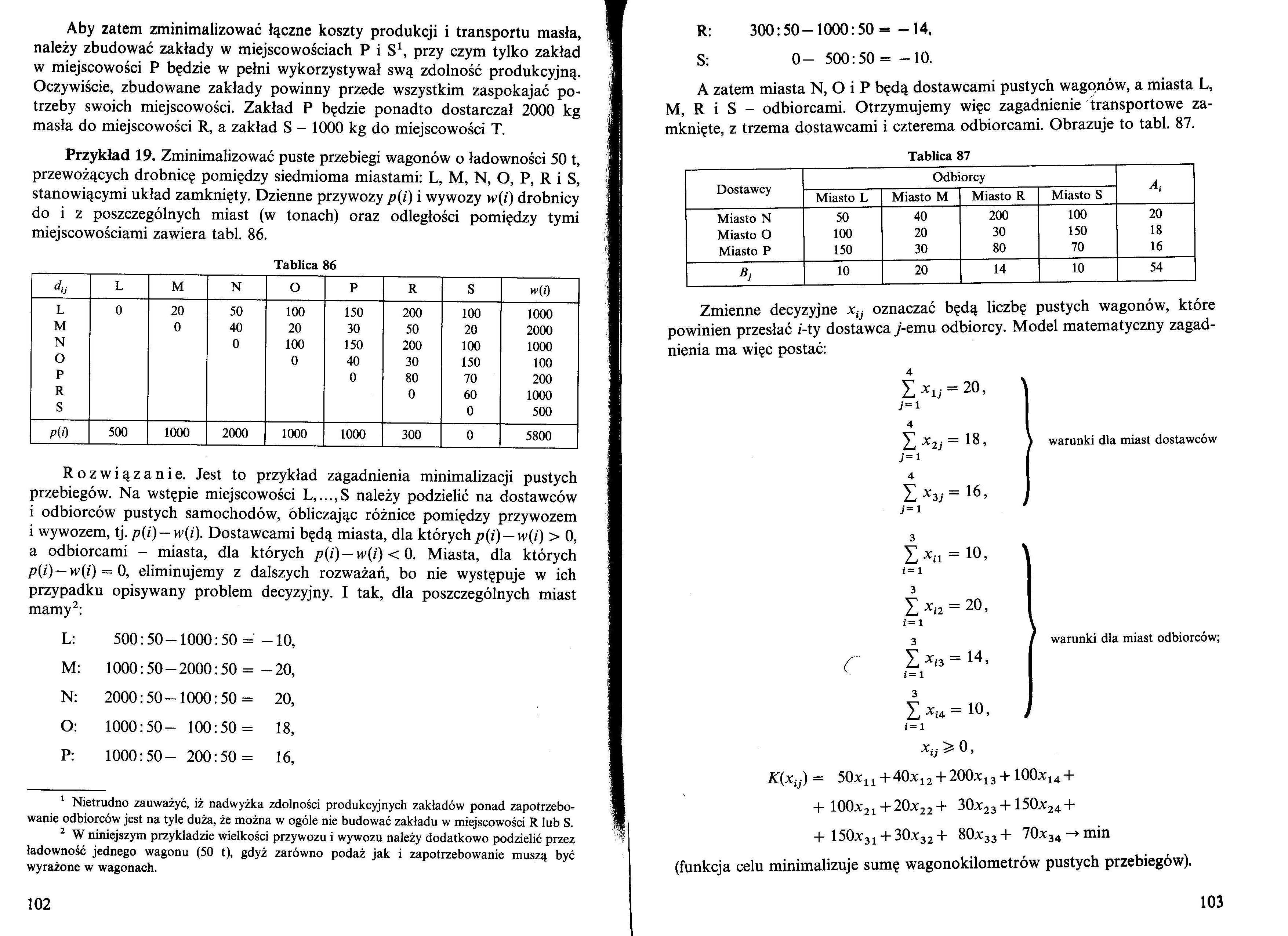
Aby zatem zminimalizować łączne koszty produkcji i transportu masła, należy zbudować zakłady w miejscowościach P i S¹, przy czym tylko zakład w miejscowości P będzie w pełni wykorzystywał swą zdolność produkcyjną. Oczywiście, zbudowane zakłady powinny przede wszystkim zaspokajać potrzeby swoich miejscowości. Zakład P będzie ponadto dostarczał 2000 kg masła do miejscowości R, a zakład S - 1000 kg do miejscowości T.

Przykład 19. Zminimalizować puste przebiegi wagonów o ładowności 50 t, przewożących drobnicę pomiędzy siedmioma miastami: L, M, N, O, P, R i S, stanowiącymi układ zamknięty. Dzienne przywozy p(i) i wywozy w(i) drobnicy do i z poszczególnych miast (w tonach) oraz odległości pomiędzy tymi miejscowościami zawiera tabl. 86.

Tablica 86

du	L	M	N	O	P	R	S	H-W
L	0	20	50	100	150	200	100	1000
M		0	40	20	30	50	20	2000
N			0	100	150	200	100	1000
O				0	40	30	150	100
P					0	80	70	200
R						0	60	1000
S							0	500
P(i)	500	1000	2000	1000	1000	300	0	5800

Rozwiązanie. Jest to przykład zagadnienia minimalizacji pustych przebiegów. Na wstępie miejscowości L,...,S należy podzielić na dostawców i odbiorców pustych samochodów, obliczając różnice pomiędzy przywozem i wywozem, tj. p(i)—w(i). Dostawcami będą miasta, dla których p(i) — w{i) > 0, a odbiorcami - miasta, dla których p(i) — w(i)< 0. Miasta, dla których p(i) — w(i) = 0, eliminujemy z dalszych rozważań, bo nie występuje w ich przypadku opisywany problem decyzyjny. I tak, dla poszczególnych miast

R:    300:50-1000:50= -14.

S:    0- 500:50= -10.

A zatem miasta N, O i P będą dostawcami pustych wagonów, a miasta L, M, R i S - odbiorcami. Otrzymujemy więc zagadnienie transportowe zamknięte, z trzema dostawcami i czterema odbiorcami. Obrazuje to tabl. 87.

Tablica 87

Dostawcy	Odbiorcy				A,
	Miasto L	Miasto M	Miasto R	Miasto S
Miasto N	50	40	200	100	20
Miasto O	100	20	30	150	18
Miasto P	150	30	80	70	16
^BJ	10	20	14	10	54

Zmienne decyzyjne x_tj oznaczać będą liczbę pustych wagonów, które powinien przesłać i-ty dostawca j-emu odbiorcy. Model matematyczny zagadnienia ma więc postać:

l warunki dla miast dostawców

Z ^xij — 20,

j=i

1*218,

j=i

Z *3j = 16,

J=1

I*ii = 10,

i = 1

Z *i2 = 20,

i = 1

warunki dla miast odbiorców;

/    Z^Xi3=l⁴-

^v    i= 1

Z*i4 = io,

i= 1

X_tj 5* o,

K(jc_(j.) = 50jc_u+40x₁₂ + 200jc₁₃ + 100x₁₄ +

+ 100x₂₁ + 20x₂₂ + 30x₂₃ + 150x₂₄ +

+ 150jc₃₁ + 30x₃₂+ 80x₃₃ + 70x₃₄ -* min (funkcja celu minimalizuje sumę wagonokilometrów pustych przebiegów).

mamy^2:
L:	500:50-1000:50 =	-io,
M:	1000:50-2000:50 =	-20,
N:	2000:50—1000:50 =	20,
O:	1000:50- 100:50 =	18,
P:	1000:50- 200:50 =	16,

103

1

   Nietrudno zauważyć, iż nadwyżka zdolności produkcyjnych zakładów ponad zapotrzebowanie odbiorców jest na tyle duża, że można w ogóle nie budować zakładu w miejscowości R lub S.

2

   W niniejszym przykładzie wielkości przywozu i wywozu należy dodatkowo podzielić przez ładowność jednego wagonu (50 t), gdyż zarówno podaż jak i zapotrzebowanie muszą być wyrażone w wagonach.