18155 MATEMATYKA148

286 V. Całka oaiacztma

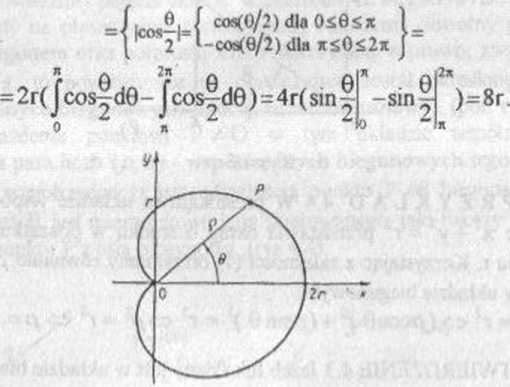
(rys 4.7). Tak nazywa się krzywą, jaką zakreśla ustalony punkt okręgu toczącego się bez poślizgu po zewnętrznej stronic drugiego nieruchomego okręgu o tym samym promieniu r. Można wykazać, żc w układzie biegunowym ma ona równanie

p - r(l-t-cosG), 0£0£2n.

Ponieważ

f²(0)+[f'(e)f = [r(l + cos0)f +[-rsin0]^J = 2r’(l + cos0) =

= 4r² cos² (0/2),

więc

2»___2k

o    o

Dodajmy, żc gdybyśmy beztrosko pominęli moduł, to wynik byłby błędny:

2n ..... 2te

|/l«2rj ^co*²y dO-2rJcos!|dO«i4rsin|J ■4r(sinJt-smO)-0.

|/|= j V4r^! cos³(0/2)d0 = 2r J|cos(0/2)|d0 =

Rys 4.7

POLE FIGURY PŁASKIEJ. Z zagadnieniem tym spotkaliśmy się już w paragrafie 1 przy' interpretacji geometrycznej całki oaiaczonej. Uogólnimy obecnie uzy skane tam wrory (1.3) i (1.4).

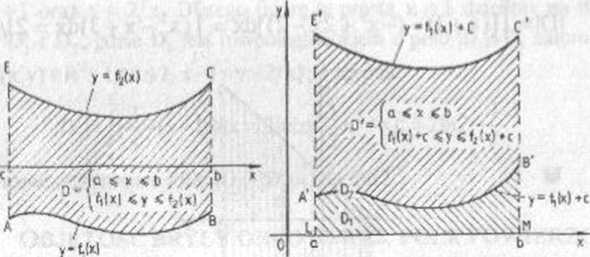
TWIERDZENIE 4.4 Jeżeli funkcje f, i f₂ są ciągle oraz f,(x)£f;(x) na przedziale <a.b>, to pole |D| figury

D*{(x,y)€R^J: a£x£b, f₁(x)iy$f₂(x)}, (por. rys 4 8), wyraża się wzorem:

b

C

y-tM

Rys 4 8

Rys 4.9

b

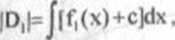
b

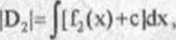
Dowód. Niech c>0 oznacza taką stałą, że f,(x)+c£0 dla x€<a,b>; wtedy również f_:(x) + c£0 dla xe<a,b>. Niech |D'|, |D,|, |D₂| oznaczają odpowiednio pola figur A'B'C'E\ LMB'A\ LMCE' na rysunku 4 9. Pierwsza z nich jest obrazem figury D= ABCE w przesunięciu o wektor [0,c]. Dlatego |D|=|D'|. Ale |D'|=P_;|-|D,|, gdzie zgodnie z wzorem (1.3)

b

więc, wobec addytywności całki względem funkcji podcałkowej, otrzymujemy

|D|=J[fi(x)+c]dx-j[f,(x)+c|dx=j|f₂(x)-f|(x)]dx.

□

co kończy dowód wzoru (4.5).