19274 PA274998

ANALIZA STATYSTYCZNA DANYCH

leżeli chcemy w łączyć jakąś grupę z porównań przypisujemy jej wagę 0. I Suma wag przypisanych wszystkim grupom musi się sumować do zera, co oznacza, że jeśli grupie pierwszej przypisalibyśmy wagę -2, to grupa druga i trzecia muszą mieć wagi +1 i +1.

W przykładzie badań, jaki omawiamy w tym rozdziale, interesowałoby nas po. równanie grupy drugiej z pierwszą i trzecią traktowanymi łącznie. Dlatego wagi, jakię powinniśmy przypisać tym grupom, mogą wglądać tak jak w tabeli 9.3.

Tabela 9.3. Przykładowe wagi dla hipotezy kierunkowej porównującej grupę drugą z grupami pierwszą i trze> tiq łącznie.

	Grupa 1	Grupa 2	Grupa 3
Waga	-1	+2	-i

Jeżeli nasza hipoteza zakładałaby, że grupa druga (relacja z tańca irlandzkiego) powinna różnić się wyłącznie od grupy pierwszej (relacja z konfliktu zbrojnego), a grupa trzecia (relacja z obrad Sejmu) jest wyłączona z porównań, to wagi dla testu kontrastów mogą wyglądać tak jak w tabeli 9.4.

Tabela 9.4. Przykładowe wagi dla testu kontrastów hipotezy kierunkowej porównującej grupę pierwszą z grupą drugą i wyłączającą z porównań grupę trzecią (dlatego waga jest 0).

	Grupa 1	Grupa 2	Grupa 3
Waga	-1	+1	0

W SPSS testy kontrastów wykonujemy klikając w głównym oknie jednoczynni-kowej analizy wariancji menu KONTRASTY. W oknie, które zostanie otwarte, musimy zdefiniować wartości współczynników kontrastu (patrz: rys. 9.15). Będziemy porównywać grupę drugą z pierwszą i trzecią traktowanymi łącznie, więc grupie pierwszej została przypisana waga -1, grupie drugiej waga +2, a grupie trzetiej waga -1. Wprowadzamy je pojedynczo w kolejności odpowiadającej kolejnośd grap.

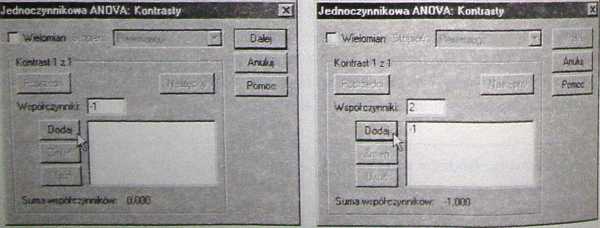
Rys. 9.15. Okno kontrastów w SPSS.

9 • JEDNOCZYNNIKOWA ANALIZA WARIANCJI...

Po wprowadzeniu pierwszego współczynnika do okienka WSPÓŁCZYNNIKI klikamy przycisk DODA) i współczynnik zostaje przeniesiony do okienka poniżej, a w okienku WSPÓŁCZYNNIKI możemy wprowadzić kolejny współczynnik.

Odczytanie i interpretacja wyników testów kontrastów nie powinna stanowić większego problemu, gdyż odwołuje się do wiedzy dotyczącej testów t-Studenta (patrz: Rozdział 8). Tabela na rys. 9.16 prezentuje wydruk wyników testów kontrastu. Odczytujemy wynik z górnego wiersza, gdyż wcześniej wykonany test Levene’a wykazał, że wariancje są jednorodne. Z tabeli na rys. 9.16 dowiadujemy się, że £(57) = 6,09; p < 0,001. Oznacza to oczywiście, że grapa druga różni się istotnie statystycznie od grup pierwszej i trzeciej traktowanej łącznie. Teraz pozostaje tylko na podstawie statystyk opisowych wskazać, która średnia jest wyższa - ta dla grapy drugiej, czv uśrednione średnie dla grap pierwszej i trzeciej.

Testy kontrastu

Kontrast	Wartość ] kontrastu ■	Błąd standardowy I	t	dr	istotność (dffus*onna>
skut Założenie o 1 równości wariancji	.2715	,04456 I	6,093	57	.000
Brak założenia o 1	.2715	.04765 |	5.698	31.971	.000

Rys. 9.16. Wyniki TESTÓW KONTRASTU.

Ortogonabuśi

kontrastów

Niekiedy mamy więcej niż jedną hipotezę kierunkową i w związku z rym chcielibyśmy wykonać więcej testów kontrastów. W takim przypadku musimy mieć na uwadze bardzo ważną zasadę budowania porównań zaplanowanych. Zasada ta dotyczy wariancji zmiennej zależnej wykorzystywanej w kolejnych porównaniach. Mówi ona, że testy kontrastów powinny być od siebie niezależne, czyli ortogonalne.

- - ' ■:

Jeżeli wykonujemy więcej niż jeden test kontrastów', to muszą być one od siebie niezależne. Możemy w związku z tym wykonać Jt - 1 porównań zaplanowanych, gdzie k oznacza liczbę grup (warunków badawczych).

Zrozumienie tej reguły będzie prostsze, jeżeli wyobrazimy sobie całą zmienność (wariancję) wyników jako duży tort. Składa się on z tylu kawałków, ile jest warunków badawczych (grup). Jeżeli dzielimy tort, to odkrawamy z całości kolejne kawałki. Niezręcznością byłoby zabierać już rozdane kawałki tortu i dzielić je ponownie. Nie popełnimy natomiast faux pas, jeżeli raz odkrojony kawał tortu podzielimy na mniejsze części.

W naszym przykładzie tort składa się z trzech kawałków - wariancja wszystkich wyników jest podzielona na trzy części ze względu na poziomy zmiennej niezależnej. Wykonując pierwszy test kontrastu wzięliśmy kawałek tortu numer 2 i zestawiliśmy go z kawałkiem 1 i 3 (kawałki te zostały potraktowane łącznie). W takim wypadku jedyne, co możemy zrobić to, podzielić kawał tortu składający się z części 1 i 3. Tak więc możemy wykonać jeszcze jeden ortogonalny test kontrastu porównujący grupy 1 i 3 ze sobą z wyłączeniem grupy 2 z tej analizy; Warunek ortogonal-