41690 PA274974

ANALIZA STATYSTYCZNA DANYCH

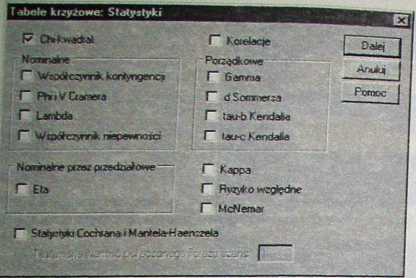
Rys. 7.13. Okno wyboru statystyk obliczanych dla zmiennych wprowadzonych do tabeli krzyżową w pakiecie SPSS.

Poprzez zaznaczenie odpowiednich pól, w' tabeli można również uzyskać procenty dla wiersza, kolumny oraz procent catośd.

W oknie STATYSTYKI można dokonać wyboru, które z testów psychologicznych będą policzone dla danych umieszczonych w tabeli krzyżowej. Tutaj właśnie znajduje się opcja, pozwalająca na wykonanie testu chi-kwadrat sprawdzającego niezależność dwóch zmiennych. Przyjrzyjmy się utworzonej tabeli krzyżowej.

Tdbctokrzyiowazifede ‘ szarlotka

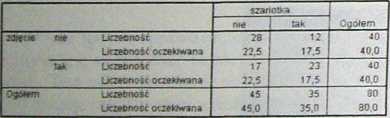
Rys. 7.14. Tabelo raportu SPSS przedstawiająca komórki tabeli krzyżowej.

Zmienna w wierszach opisuje technikę stosowaną przez kelnerkę - albo sam opis ciastka, albo opis wraz ze zdjęciem. Zmienna w kolumnach mów o zachowaniu klientów, którzy zamówili bądź nie zdecydowali się na zamówienie szarlotki. Na przecięciu wierszy i kolumn wyświetlone są liczebności osób dla wszystkich możliwych kombinacji obu zmiennych. Odczytującnp. wartość z miejsca przecięcia się drugiego wiersza i drugiej kolumny można dowiedzieć się, że były dwadzieścia trzy osoby, które widząc zdjęcie szarlotki zdecydowały się na jej zakup.

W tej samej tabeli jako liczebności oczekiwane podane są wartości teoretycznego rozkładu losowego dla wprowadzonych do tabeli zmiennych-wliczone na podstawie uzyskanych danych. Rozkład teoretyczny, oczekiwany jest rozkładem, który pojawiłby się jako obserwowany, jeśli między zmienny-

mi nie byłoby żadnych zależności. W jaki sposób obliczane są wartości oczekiwane dla dwóch zmiennych? Służy do tego poniższy — bardzo podobny do poprzedniego wzór.

Wzór służący do obliczania wartości oczekiwanych dla komórek tabeli krzyżowej...

(7.3)

10, x iOj

kr 20

Gdzie:

Ł; - wartości oczekiwane (ang. expected) dla komórki na przecięciu rzędu ,i" oraz kolumny.) Oi - wartości obserwowane dla rzędu ,i"

Oj - wartości obserwowane dla kolumny 0 - wszystkie wartości obserwowane

Według wzoru, aby policzyć wartości oczekiwane dla danej komórki, należy pomnożyć przez siebie sumy krańcowe wartości obserwowanych z właściwych dla tej komórki rzędu i kolumny, a następnie podzielić przez sumę wszystkich wartości obserwowanych. Gdy znane są już wartości oczekiwane i obsenwwane, można dokonać obliczeń wartości testu chi-kwadrat. Wzór na statystykę chi-kwadrat jest identyczny jak w omówionych vvcześniej przypadkach.

Podstawienie danych z przykładu do wzoru na test chi-kwadrat.

, „(O-f)²    (28-22,5)2 (12-17,5)2 (17 - 22,5)2 (23-17,5)2    ,,

* =2— ⁼ —22,5    ⁺    17^5    ⁺ —22fi~ ⁺~iTj- = ⁶*¹⁴⁶    (7A)

Wartość testu jest także liczona w sposób automatyczny i raportowana wraz z poziomem istotności w odpowiedniej tabeli (rys. 7.15).

Testy Chi-kwackat

	Wartość	df	Istotność asymptotyezn a (dwustronna)	istotność doidadna (dwustronna)	istotność dokładna Oednostr onna)
CM-lwadral Pearsóna	6.146^b	1	.013
Poprawka na ciągłość^3	5,079	1	,024
Borę wiarygodności	6,233	1	.013
DoWadny test Fishera				,024	,012
Test związku liniowego	6,069	1	,014
NWfcnyth obserwacji	80

a Obliczone wyłącznie dla tabeli 2x2.

b ,0% komórek(0) ma liczebność oczekiwaną mniejszą niż 5. Minimalna liczebność oczekiwana wynosi 17,50.

Rys. 7.15. Tobelo raportu SPSS przedstawiająca statystyki obliczone dla zmiennych wprowadzonych do tabeli krzyżowej.

Powyższa tabela przedstawia wartość testu chi-kwadrat równą x~ (1, N = 80) = 6,15; p < 0,05. Oznacza to, że dopuszczalne jest odrzucenie hipotezy zerowej mówiącej o niezależności analizowanych zmiennych i przyjęcie hipotezy o istnieniu związku między tymi zmiennymi. Istnieją zatem