23307 PC043388

Metoda przeciwnych współczynników

W tej metodzie postępujemy następująco:

1)    Mnożymy równania układu przez tak dobrane liczby, by wspólc2ynri3$L co najmniej jednej zmiennej w równaniach były liczbami przeriwnyngiB

2)    Dodajemy równania stronami, otrzymując jako „sumę” równanie z niewiadomą.

3)    Rozwiązanie tego równania podstawiamy do dowolnego równania uktade otrzymując drugą z szukanych współrzędnych rozwiązania.

PRZYKŁAD 1.80

Abv zastosować metodę pizeciwnych współczynników do rozwiązania ukladt

5x-2y=9 3x+y = 1

drugie równanie tego układu pomnożymy stronami przez 2, uzyskując

5r-2y=9

6x+2y=2

Dodając teraz stronami równania:

|5*-2y=9 [óx+2y=2 llx =11

otrzymujemy równanie postaci lir =11, którego rozwiązaniem jest zfi Podstawiając otrzymaną wartość do dowolnego równania układu, dostajesf y - -Z a stąd mamy ostateczne rozwiązanie: x = 1, y=—2.

Metoda graficzna

Metoda ta jest metodą przybliżoną. W celu określenia liczby rozwiązań^* ewentualnie przybliżonej wartości liczb tworzących rozwiązanie wykonują® następujące operacje:

1)    Traktujemy oba równania układu jak równania prostych i zapisujemy j* w postara kierunkowej (o ile to możliwe).

2)    Szkicujemy proste w układzie współrzędnych.

3)    Na podstawie wykresów równań odczytujemy liczbę rozwiązań i wspótaędf punktu wspólnego dla obu prostych (jeśli istnieje jeden taki punkt). 'Ą

Przykład 1.81

Aby zastosować metodę graficzną do układu z przykładu 1.79, przekształcimy równania do postaci kierunkowej:

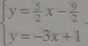
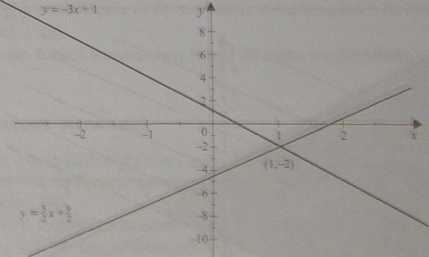
Szkicujemy obie proste w układzie współrzędnych. Z ilustracji 1.41 odczytujemy, że istnieje jeden punkt wspólny tych prostych - punkt o współrzędnych (1,-2).

Ilustracja 1.41. Interpretacja graficzna układu równań z przykładu 1.81

Metody podstawiania oraz przeciwnych współczynników można z powodzeniem stosować dla układów równań o większej liczbie równań lub większej liczbie niewiadomych.

Układy nierówności

Z układem dwóch nierówności liniowych mamy do czynienia w sytuacji, gdy w układzie równań (1.8) znaki równości zastąpimy znakami nierówności (silnej lub słabej). Rozwiązaniem układu nierówności będzie ta część płaszczyzny