DSC00084 (18)

dla zmiennego przepływu, kondensatu. Przeciętny współczynnik znajdziemy przy pomocy następującego rozumowania.

Obliczmy ciepło oddane przez kondensującą parę na całej długości rury. Wynosi ono

oc .fi . At = l . r

no    o

gdzie:    -

przepływ wagowy na jednostkę obwodu rury u dołu rury;

At =

tp - t_g - różnica temperatur pary i ścianki; wysokość rury;

średni współczynnik konwekcji dla całej długości rury;

Ł I A dla

ciepło kondensacji pary. różniczkowego odcinka dH

. a t . dH = L.d r

* O

Po podzieleniu obydwu równań przez siebie otrzymujemy

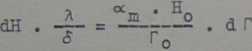
a po wprowadzeniu wartości $

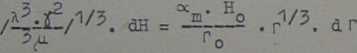
Scałkujmy to równanie w granicach 0-H_Q i 0— r_Q.

liii

cc .H

1 i i TT-^ro‘^ro

1/3.

:V3

Hfi

mm i 0.925 i

V r„.iu

J ' o t

Otrzymamy

oc.

i i ./sL^/V3 l i .

.T

JLiJ_L_/V3

ot _.r.

⁴/i3 _¥2 ,

oc = O.WV--4v‘p¹ a * a m . at.E ‘    o

\7 prawej stronie równania znane są nam wszystleie elementy oprócz A t.*0tóż aby wyznaczyć <*_ i a t posługujemy się metodą prób i błędów: zakładamy a t, przy jego pomocy znaj -dujemy cc _n z odpowiedniego wzoru, potem określamy sunarycz -ny współczynnik przenoszenia ciepła k, następnie wyznaczany temperaturę ścianki i otrzymujemy At, które powinno odpowiadać a t założonemu.. Jeśli nie odpowiada - próbujemy dobierać nowe a t aż do pomyślnego rezultatu.

Podobnie można wyprowadzić równanie dla oc dla rur poziomych.

li i    S

gdzie d - średnica rury.

Jednak, gdy wyprowadzone teoretycznie wzory sprawdzono na drodze doświadczalnej, to okazało się, że x dla rur poziomych zgodne jest z wynikami doświadczeń, natomiast dla _m uzyskania podobnej zgodności z doświadczeniem wzoru na a _a rur pionowych należy zwiększyć współczynnik liczbowy przed pierwiastkiem. Niżej podajemy poprawiony wzór Nusselta na x_a dla rur pionowych

U i n    * B

Wprowadzona przez IJusselta poprawka daje się uzasadnić występowaniem sił napięcia powierzchniowego.

Dla wody - wzory /128/ i /129/ przedstawiono w następującej postaci, znacznie wygodniejszej dla obliczeń rachunkowych

85

1

więc możemy znaleźć oc_m, jeśli znamy tj. jeśli znamy ilość pary kondensującej na 1 m obwodu rury.

Moż.ęmy również wyznaczyć ot_m, jeśli znamy At. Znajdźmy ?o ^z r6wnanaa ^ocm»H₀. At = L. P_Q i podstawmy w równanie naoc^.