27451 skrypt3

Cyfrowa ru tnA«iA aum i*-v •u.---"<

A

(6.2)

< y\r = \y >V- (yo >r)

A więc < y\_T stanowi wektor wierszowy próbek Operację sumy elementów określimy jako

|* >_r + |y >T= l«r+y >r= I ^r» ' V0 *t + vrl'

„ operacje mnożenia pr/ez5kalnr o t%_ zdefiniujemy jako

|v >ro* fyoa ■ • yr" I'

Mając wektory \x >r i b >r. wprowadźmy iloczyn skalamy ,ako

r

< jtly >r= N •• • ^xr][yo ■ ■ ■ yrY- 7L*'^y'

(6.3)

(6.4)

(6.5)

Notacja

Majac |y >r. zdefiniujmy operator opóźnienia jako

|ry >_T= [Oyo ... yr-,]'

skąd wniosek. Ze

|z*y >r= [0_2 yo ... _yr._t]'

Wprowadźmy rodzinę podprzestrzeni

S,_XJ = jpfln{|z^łv>r....,|z*y>_r)

(6.14)

Niech

indukujący normę

IIIy>r \\=<y\y>l= (l>?)

(6.6)

\Y,.k >t= t |z'y >r ... |**y>r]

Wówczas operator projekcji ortogonalnej na S_/>;7- będzie wyrażony jako

P(Si,k.r) = I^Yi.k>r< Yi.Mjc >}*< Yi.k\r    (6.16)

(6.15)

oraz metrykę

,/(|<>r.|y>r) = IIU>r-|y>7- || = || |x-y >7 11 =

- <x-y\x-y >}=

Operator projekcji ortogonalnej na span{\y >7} W™ wyrażony jako

P[\y>r) - l.v>r< >*l.v >7 '< >'l^

sknd wniosek, że projekcja ortogonalna wektora |x >r na span{\y >7}. »o

\t >t= P(\y >t)\^x >t= I y >r< y\y >t ¹ < *1* ^>T= \y^>r P

Niech

k>r=(0—5 if

(6.7)

gdzie < Y_lJc\Y_ik >_T ¹ może być rozumiane w sensie macierzy pseudoodwrotnej Traktując |r'y >_T,    ,|z*y >7 - zgodnie z (6.14) - jakobazę tej podprzestrzeni.

jej dowolny element będzie wyrażony jako

>t= Iz'y >r /*+ .. + |z*y >r /*

(6 17)

Wówczas dla elementów |</> >_r oraz |y/ >_T (gdzie 11// >_r wyraża się za pomocą (6.17) z/„. ./V zamienionymi na g,. .. ,g*)mamy

< *| V >T= LA A] < YidYiJc >T [gi gk\

(6.18)

gdzie < Y_ik\Y_ik >r jest macierzą Grama elementów |z*y .,|z*y >_T. Stąd i z (6.6) wynika, że

II* >r II² = [//•• • fk] < Y,.k\Y,.k >r[fi ■ ■ fk}'

(6.19)

Uwaga: Zauważmy, ze przestrzenie S_iik = span{y(t - i).. ,y[t - fc)} (gdzie y(t — j) są zmiennymi losowymi stacjonarnego ergodycznego sygnału losowego y) i (6.14) są (asymptotycznie) izomorficznie izornetryćzne W istocie

I. y(t - j) f+ \z^Jy>_T

Wówczas

< n\y >7= >i

(6.1D

2. (y(r - f),y(r - /)) = Ey(t - j)y(r - /) = lim - < z>y\z^ly >_T

I —*ro I

132

(ccdim

133

sniiłHł

Cyfrowa filtracja adaptacyjna szeregów czasowych

skąd wniosek, ie

lly(' - »II^J = lim ^ < r^yy|.^Jv >_T

7 —*w /

j = i,..._tk

W konsekwencji, jeśli rozważyć elementy $,'(/£ S,_ik, gdzie 0 = f,y(t    -f f_kv(t - k)

V = giyU-i) + ••• + £*>'('-*)

m

Rys

Liniowa prognoza śREDNiOKWApnArowA szeregów czasowych

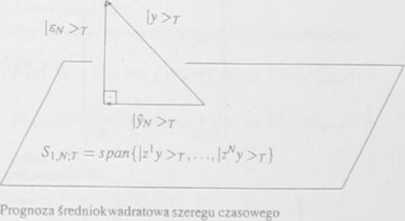
oraz elementy |0 >7, |i/r >r€ Sj^-j (6.17), to

I

(*. V) = Jim - < 0|v' >7

7 -*rt> I

a zatem:

/    >T

2.

^{1,2 =}/i"f¹¹

Poszukiwany estymator prognozy

l>V >7= [>W.o ... 9n,tY

(6.20)

wyraża się jako projekcja ortogonalna elementu |y >7 na podprzestrzeti S\_tfjj rozpiętą na przeszłości {|r^ły >7,..., |r^Ny >7}

|y/Y >r = r(5i,At;r)|y >r=

= \Y\,K >r< ^'i./V|>'1 .AZ >f’< YlJi\y>T € Stjij

(6.21)

Powyższa obserwacja umożliwia bezpośrednie przeniesienie uprzednio rozważanych algorytmów ortogonalnej prognozy/filtracji innowacyjnej w przestrzeni rozpiętej na zmiennych losowych obserwowanego sygnału losowego do przestrzeni rozpiętej na próbkach jego pojedynczej realizacji Jest to przedmiot kolejnych paragrafów niniejszego rozdziału, w których zostanie wykazane, iż uprzednio wyprowadzone algorytmy cyfrowej filtracji ortogonalnej sygnałów losowych reprezentowanych za pomocą zmiennych losowych „optycznie” pozostają niezmienione, jeśli obserwacje stanowią nabór próbek pojedynczych ich realizacji

Liniowa prognoza średniokwadratowa szeregów czasowych

Niech będzie dany wektor |v >7 próbek {yo, ... v*7 } rzeczywistego szeregu czasowego. obserwowanego na skończonym odcinku czasu {0,.    ,7 } Przyjmie

my, że obserwowany szereg czasowy jest lewostronnie okienkowany (v , ó. t •- 1,2,    .). Problem liniowej prognozy śicdniokwadratowcj szeregu czaso

wego przedstawiono na rys 6 I

i jako element peniprzestrzeni S\j^j - stanowi kombinację liniową elementów

jej bazy

I9n >7=12')'>7 ow., + • • + I/'y>7 on.n

Innymi słowy mamy

>W.f = yr-i ow, 1 +... + yt-N&NJł . ¹ — 0,...»7 Z elementem | \_N >7 jest stowarzyszony wektor błędu prognozy \gn >t= [g/y.o .. • £/v.rr który zgodnie z rys 6.1 wyraża się jako

|«/V >r= P(St_N.r)\y >r= l.v >t -19* >r J- *.*r

lub. biorąc pod uwagę (6.22). jako

\s_N >_T= |y >r -l-|-*.v >r «a».i + • •• +1**? ^>r “w

(6.22)

(6.23)

(6.24)

(6.25)

134