27751 IMG„64

Kierunek: informatyka, studia dzienne magisterskie wytmy i struktury danych, xcm.II

ImiÄ™ i nazwisko

...    _h ^gorytnihw.

^J- Poniżej przedstawiono oszacowania rzeczywistej (technicznej) zÅ‚ożonoÅ›ci czasowej pewny*-" *    . _c §jÄ™

Na podstawie tycli oszacowań określ asymptotyczny złożoność czasową tych algorytmów. p -notacją wielkie O (odpowiedź uzasadnij:

(a) 5*tr^Å‚ - J0*n²+6*n + 12    ...........................................................................................

(b)    8+2*n* + 1.5*2^rt    ...........................................................................................

2. Skorzystaj z metody rekurencji uniwersalnej i pokaż, źe rozwiązaniem rekurencji T(n) " 4 r(n/2) ^T wyszukiwaniu binarnego jest T(n) ~ B(lg n).

3* Co realizuje lunkcja fl i co otrzymamy w wyniku jej wykonania 7 OkreÅ›l klasÄ™ zÅ‚ożonoÅ›ci 00 ^ⁱⁿ P (algorytmu) fl.

for i:-l to r-1 do begin

lf m < t[i] then zn s- t (i]

elae if n > t(ij then n im tli)

end;

end;

begin

f 1 (a, 10, zn, n) ; end.

prgram 9;

const as array f0.. 9] ot integer *

(4,7,3,1,2,0,9,12,0,5); var m, n: integer;

procedura fl(trarray ot integer; r: integer;

var m, n:integer);

var

i: integer; begin

m :• t [0]; n t [0] ;

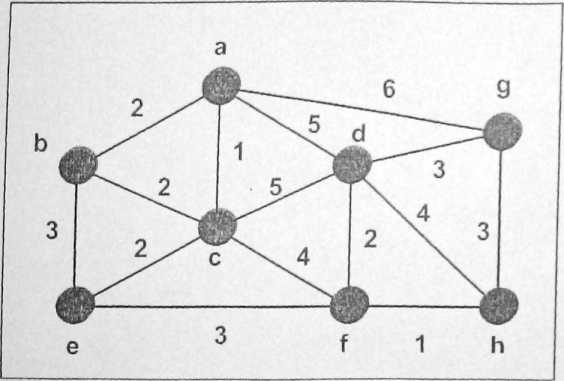
4. Dla poniższego ważonego grafu nicskicrowancgo wyznaczyć minimalne drzewo rozpinające (MST). . posługując się algorytmem Kruskala..

Załóżmy, że wraz z partnerem grasz w zgadywanie liczby naturalnej z przedziaÅ‚u f 1,1024]. Partner wybiera dowolna liczbÄ™ z tego przedziaÅ‚u, a Ty próbujesz jÄ… zgadnąć. Partner może jedynie odpowiadać: tak. zu maÅ‚a, za duża. JakÄ… przyjmiesz strategiÄ™ odgadywania liczby, by jÄ… znaleźć w możliwie najmniejszej liczbie prób? Ile tych prób musisz wykonać, jeÅ›li Partner wybraÅ‚ liczbÄ™ I 177.

Dana jest następująca funkcja rckurencyjna:

function GCD (i.j: integer): integer;

{ Funkcja zwraca największy wspólny dzielnik dwóch licz całkowitych i oraz jf begin

ifi mod j - 0 then GCD:~j else

GCD := GCD (j, i mod j); end; ( GCD f

-3 -