46269 IMG„63

Kierunek: informatyka, studia cbienne magisterskie A/guiy/my i simki wy danych, sam. II

7. Dla poniższej sieci połączeń między miastami wyznaczyć minimalną ścieżkę z miasta a do k, posługując strategią programowania dynamicznego. Podaj wszystkie optymalne rozwiązania.

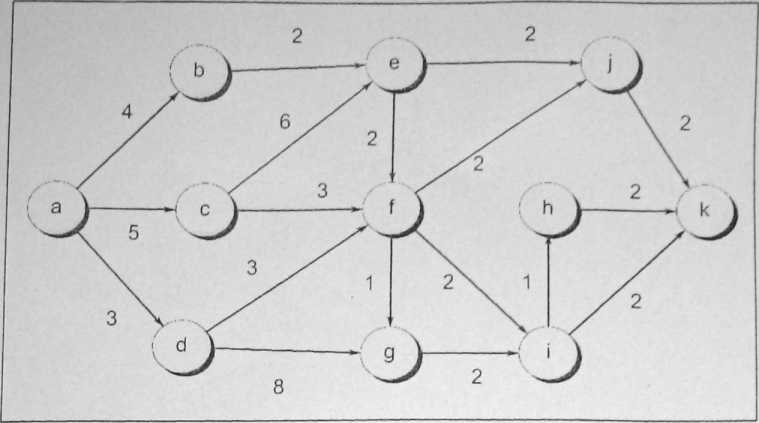
8.    Profesor Midas jedzie samochodem z Newark do Reno. Bak peÅ‚en benzyny w jego pojeździe wystarcza na przejechanie n km, a na jego mapie sÄ… zaznaczone odlegÅ‚oÅ›ci miÄ™dzy wszystkimi stacjami benzynowymi na trasie. Profesor ma zamiar tankować jak najmniejsza liczbÄ™ razy w trakcie podróży. Podaj efektywnÄ… metodÄ™, za pomocÄ… której profesor Midas może (z góry) ustalić, na których stacjach powinien tankować, oraz udowodnij, że strategia ta prowadzi zawsze do rozwiÄ…zania optymalnego.

9.    Zaprojektuj algorytm typu dziel i zwyciężaj do znajdowania /7-tcj co do wielkoÅ›ci liczby spoÅ›ród m liczb (liczby tc nie sÄ… posortowane), gdzie n jest zmiennÄ…. Wskazówka! Wybierz dowolna liczbÄ™ z ciÄ…gu, i nastÄ™pnie podziel wyjÅ›ciowy ciÄ…g liczb na trzy podciÄ…gi: mniejsze od wybranej liczby, równe jej i wiÄ™ksze od niej. PodciÄ…gi prawy i lewy uporzÄ…dkuj rosnÄ…co, dzielÄ…c jc dotÄ…d dopóki sortowanie stanie siÄ™ oczywiste, a nastÄ™pnie przystÄ…p do fazy Å‚Ä…czenia. PamiÄ™taj, żc masz znaleźć tylko /i-tÄ… co do wielkoÅ›ci liczbÄ™, co oznacza, ż.c możesz w odpowiednim momencie Å‚Ä…czenie przerwać. Zilustruj każdy krok swojego pomysÅ‚u na przykÅ‚adzie przedstawionego ciÄ…gu liczb, w którym masz znaleźć 7-tÄ…co do wielkoÅ›ci liczbÄ™:

25, 4, 3, -1,5, 8,5,3, 4, -5 16.

10.    Udowodnij, źe

1;

1;

{(s«-c + t) a (t Å› y)} while t ^ y do spec S i.—s + t<—t + endspec {s<—c + y}