35257 IMG„65

Kierunek: informatyka, studia dzienne magisterskie Algorytmy i struklwy danych, nem. 11_

Pokaż, jak wygląda drzewo wywołań funkcji GCl), gdy wywołamy ją następująco: CCO (15. V)

7. Dla poniższej sieci poÅ‚Ä…czeÅ„ miÄ™dzy miastami wyznaczyć minimalnÄ… Å›cieżkÄ™ z miasta a do k, posÅ‚ugujÄ…c strategiÄ… programowania dynamicznego. Podaj wszystkie optymalne rozwiÄ…zania.

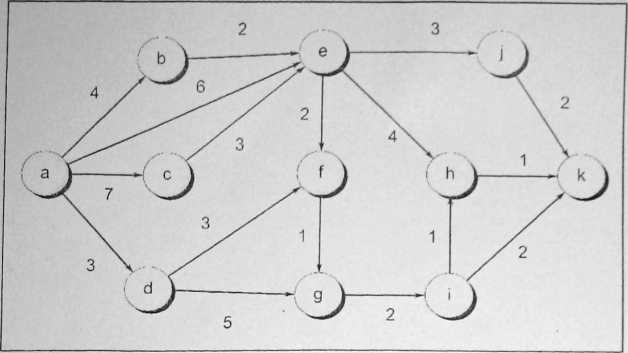
8.    Przypuśćmy, żc w dyskretnym problemie plecakowym kolejność przedmiotów uporzÄ…dkowanych rosnÄ…co wedÅ‚ug ciężaru jest taka sama, jak przy uporzÄ…dkowaniu malejÄ…cym wedÅ‚ug wartoÅ›ci. Podaj efektywny algorytm znajdujÄ…cy optymalne rozwiÄ…zanie dla lej wersji problemu plecakowego i uzasadnij jego poprawność.

9.    Zaprojektuj algorytm typu dziel i zwyciężaj do znajdowania /7-tej co do wielkoÅ›ci liczby spoÅ›ród m liczb (liczby tc nic sÄ… posortowane), gdzie n jest zmiennÄ…. Wskazówka! Wybierz dowolna liczbÄ™ z ciÄ…gu, i nastÄ™pnie podziel wyjÅ›ciowy ciÄ…g liczb na trzy podciÄ…gi: mniejsze od wybranej liczby, równe jej i wiÄ™ksze od niej. PodciÄ…gi prawy i lewy uporzÄ…dkuj rosnÄ…co, dzielÄ…c jc dotÄ…d dopóki sortowanie stanic siÄ™ oczywiste, a nastÄ™pnie przystÄ…p do fazy Å‚Ä…czenia. PamiÄ™taj, żc masz znaleźć tylko /i-tÄ… co do wielkoÅ›ci liczbÄ™, co oznacza, żc możesz w odpowiednim momencie Å‚Ä…czenie przerwać. Zilustruj każdy krok swojego pomysÅ‚u na przykÅ‚adzie przedstawionego ciÄ…gu liczb, w którym masz znaleźć 5-tÄ… co do wielkoÅ›ci liczbÄ™: -1, 24, 21, 5,-2, 8, 9, 25, 4, 17 16.

10.    Udowodnij, że

{(x > 0) a (y > 0)} spec zf— 0;

Uf—Xj repeat z<—z + y;

Uf—u - 1; until u | 0 endspec {zf-x*y}