31905 skrypt031

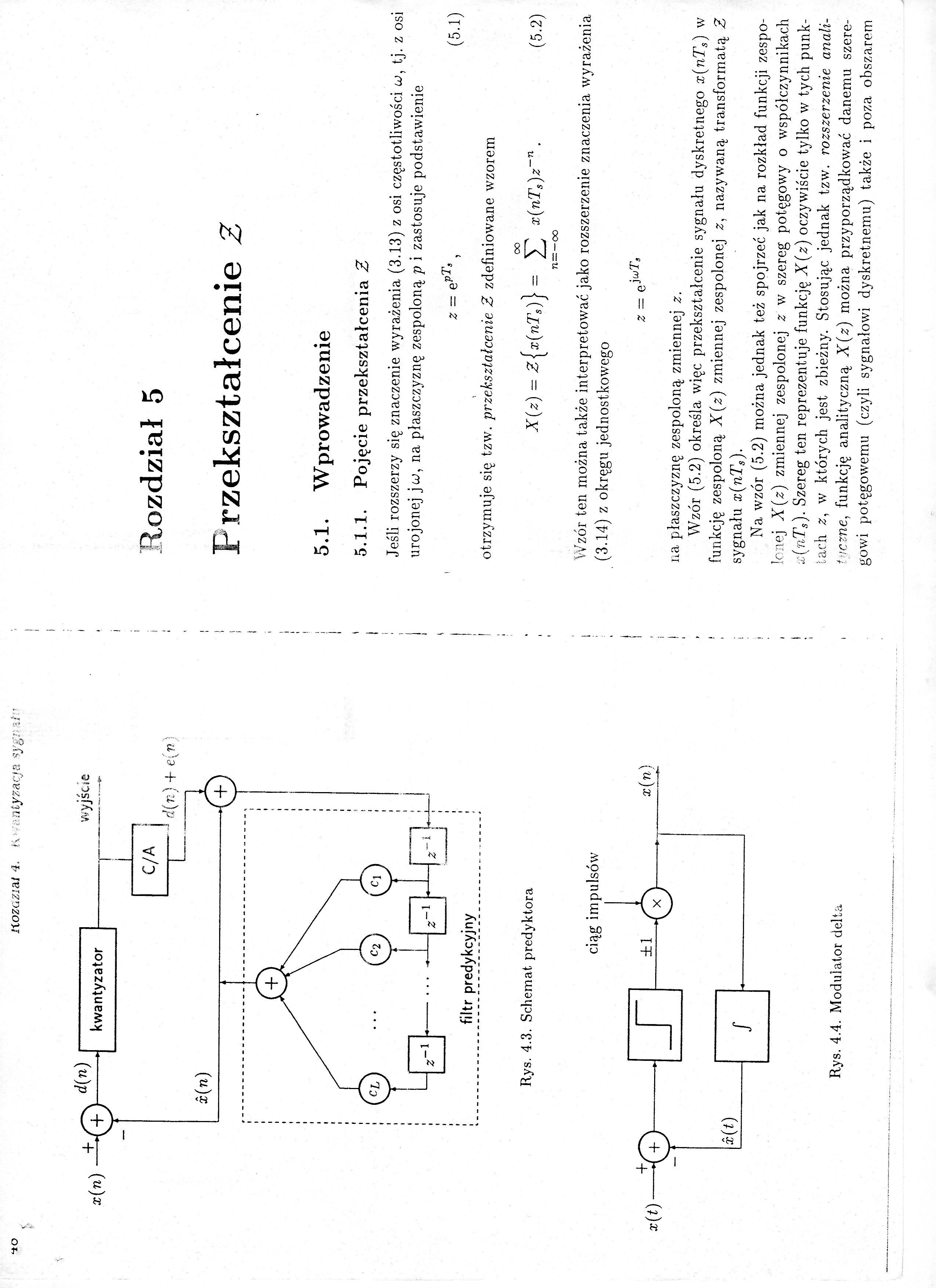
•±o nozaziat 4. *•. atyracja sygi

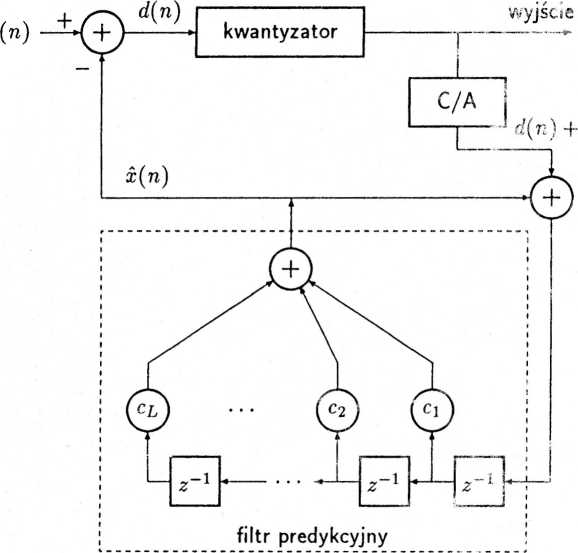
Rys. 4.3. Schemat, predyktora

ciąg impulsów

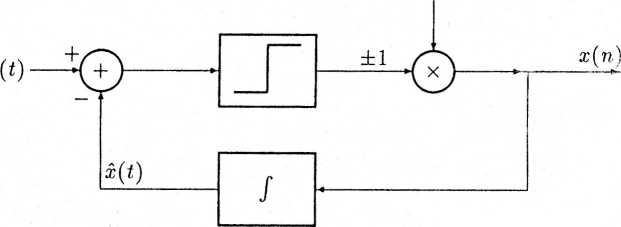
Rys. 4.4. Modulator delta

Rozdział 5

Przekształcenie Z

5.1.    Wprowadzenie

5.1.1.    Pojęcie przekształcenia Z

Jeśli rozszerzy się znaczenie wyrażenia (3.13) z osi częstotliwości u>, tj. z osi urojonej j w, na płaszczyznę zespoloną p i zastosuje podstawienie

z = e^pTs,    (5.1)

otrzymuje się tzw. przekształcenie Z zdefiniowane wzorem

OO

X(z) = z{x(nT,)}= £ x(nT_s)z~ⁿ.    (5.2)

Tl— — OO

Wzór ten można także interpretować jako rozszerzenie znaczenia wyrażenia (3.14) z okręgu jednostkowego

z = e^jwTs

na płaszczyznę zespoloną zmiennej 2.

Wzór (5.2) określa więc przekształcenie sygnału dyskretnego x(nT_s) w funkcję zespoloną X(z) zmiennej zespolonej z, nazywaną transformatą Z sygnału x(nT_s).

Na wzór (5.2) można jednak też spojrzeć jak na rozkład funkcji zespolonej X(z) zmiennej zespolonej z w szereg potęgowy o współczynnikach x(nT_s). Szereg ten reprezentuje funkcję X(z) oczywiście tylko w tych punktach z, w których jest zbieżny. Stosując jednak tzw. rozszerzenie anali-ttczne, funkcję analityczną X(z) można przyporządkować danemu szeregowi potęgowemu (czyli sygnałowi dyskretnemu) także i poza obszarem