34858 Untitled Scanned 24 (9)

3) Przemieszczenia (współczynniki i wyrazy wolne) będą miały wartości równe zeru, jeżeli tak dobierzemy układ podstawowy, aby rzędne jednego wykresu przyjmowały wartości równe zeru na wysokości środka ciężkości innego wykresu. W tym celu wprowadzamy (myślowo) nieskończenie sztywne wsporniki.

Dla ramy symetrycznej z rys. 13.24a przyjmujemy układ zastępczy pokazany na rys. 13.24b. Wykresy momentów od jednostkowych wartości niewiadomych sił pokazano na rys. 13.24c-?-e.

Ponieważ założyliśmy, że wspornik ma sztywność równą nieskończoności (EJ= oo), nie ma więc potrzeby obliczania całki dla wspornika, gdyż niezależnie od wartości mo

f

1

mentów

EJ J

Mj M_k dx=0. W tym przypadku wartości zerowe przyjmą współczynniki

ó₁₂, S_l3 i S₂3, jak również symetryczne względem nich S_2l, ó₃₁, ó₃₂.

Przykład zastosowania nieskończenie sztywnych wsporników dla ramy niesymetrycznej z rys. 13.25a pokazano na rys. 13.25b. Wykresy momentów jednostkowych pokazano na rys. 13.25c, d, e. Przy takim układzie podstawowym otrzymamy:

ńi₂—5₂₁—ń₁₃—ń₃₁—ń₃₂—ń₂3—0

i w efekcie pełne rozdzielenie niewiadomych.

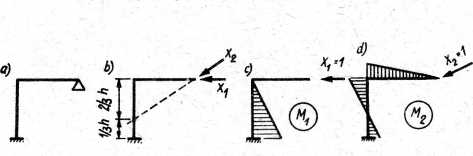
Na rys. 13.26a pokazano ramę, dla której bez wprowadzania sztywnych wsporników możemy tak dobrać układ zastępczy (rys. 13.26b), że rzędne jednego wykresu przyjmują wartość zero (rys. 13.26d) na wprost środków ciężkości wykresu drugiego (rys. 13.26c).

Inną ramę niesymetryczną pokazano na rys. 13.27a. W tym przypadku dla uzyskania jak największej liczby współczynników (w równaniach kanonicznych) równych zeru, zastosujemy kilka nieskończenie sztywnych wsporników. Odpowiedni układ zastępczy pokazano na rys. 13.27b, a wykresy momentów od jednostkowych niewiadomych na rys. 13.27c-^h. Linię działania siły X₃ dobieramy tak, aby łączyła środki ciężkości słupów AB i DC, a linię działania siły X₆ jako łączącą środki ciężkości słupów CD i FG. Otrzymamy wówczas:

^14—^16 — ń₂₄ —<5₂₅ —^26 — ^34 — ^35 ~0 •

Rys. 13.26

Sposób powyższy okaże się jeszcze bardziej przydatny dla ramy symetrycznej pokazanej na rys. 13.28a. Rozmieszczenie niewiadomych pokazano na rys. 13.28b; wykresy momentów dla stanów X₁ — l /.. X₆ = l — na rys. 13.28c-hh. Otrzymamy tu:

^13 ⁼^14 ⁼ ^15 ⁼^23 ⁼^24 ⁼ ^25 ~^26 ⁼ ^35 ⁼ ^36 ⁼⁼^45 ⁼^46 ⁼0-

462